A gentle introduction to LoRA for fine-tuning large language models

Large language models are trained in a pretraining-finetuning fashion, where general language concepts are learned first on large corpora, after which model training is continued for task-specific behavior. LLM scaling laws suggest that larger models tend to produce better results than smaller ones, and hence models have become larger these past few years. This puts stress on finetuning, because increasingly powerful hardware is require.

In this article, we're looking at Low-Rank Adaptation or LoRA, which attempts to mitigate parts of these hardware requirements by finetuning in a smart way. Theorizing that weight matrices lose their column and row uniqueness (i.e., their full rank) during finetuning, the authors of the LoRA paper suggest that matrices of weight updates can hence be decomposed in two low-rank matrices that together compose the original update matrix. This way, model parameters can be reduced extensively.

It's structured as follows. Firstly, we'll look at pretraining and finetuning, to (re)discover what they are in the first place - or for setting the scene, for those who don't yet know what they are. This is followed by looking into problems encountered when finetuning increasingly large language models. Subsequently, LoRA is introduced, and you'll read about why it reduces the hardware requirements for finetuning.

Are you ready? Let's take a look 😎

A recap: what are pretraining and finetuning?

Ever since the rise of Transformer architectures in machine learning, pretraining a model followed by finetuning has been a widely used paradigm. In fact, its usage has led to many of the innovations that we have observed in the past few years. This article discusses LoRA, which can be used for finetuning large models without the need for spending a large amount of money on computational resources.

But before we introduce LoRA, it's important to set the scene - what are pretraining and finetuning?

Assuming that you have a basic understanding of Transformers, let's take a look at the BERT architecture:

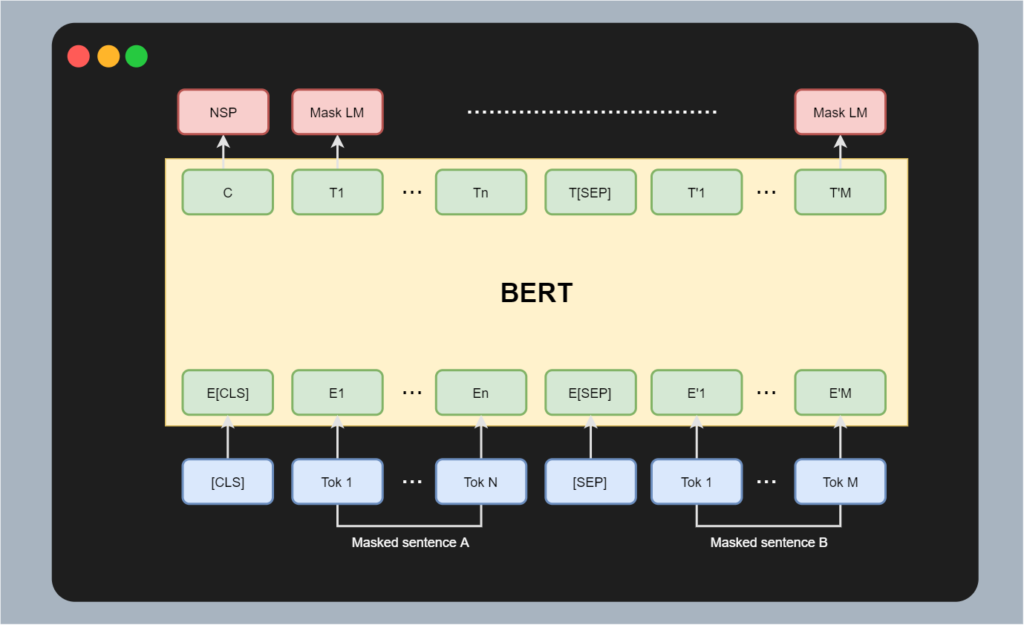
This architecture comes in two flavors, BERT Base and BERT Large. Compared to other really large models today, BERT's number of trainable parameters is relatively small - but 110 and 340 million parameters is still quite a big number, to be honest.

Recall that BERT architectures are used for thorough understanding of text, primarily the semantics - hence their use at Google and its embedding in Google Search.

Training the original BERT models was done by taking a large dataset that was scraped off the internet, tokenizing it and then feeding it for masked language modelling: trying to predict masked tokens, hence letting it understand the semantics of text. This is done in a relatively self-supervised fashion, and there is no single task that BERT solves at the time. This is called pretraining: it allows large language models to deeply model relationships in text.

Mathematically, after training, you end up with a model that has weights \(\mathbf{W}\) (distributed over many individual layers).

Now suppose that you'd like to use BERT for a specific task. Say that you are working at a news organization, where you're using machine learning to classify news articles into a discrete class - that of newsworthiness (suppose 0 - not newsworthy; 1 - newsworthy; 2 - very newsworthy).

For this, you have created a dataset with pairs of texts and their newsworthiness. You load BERT into your favorite machine learning framework and continue training so that BERT learns to adapt to the task at hand. Now, you're finetuning the model to that specific task at hand.

Finetuning means following the high-level machine learning process: feeding a batch of samples through the model (a forward pass), computing loss, backpropagating the error through the network, and adapting the model weights according to your optimization strategy. You do this many times, until you either run out of iterations (epochs) or reach a different metric.

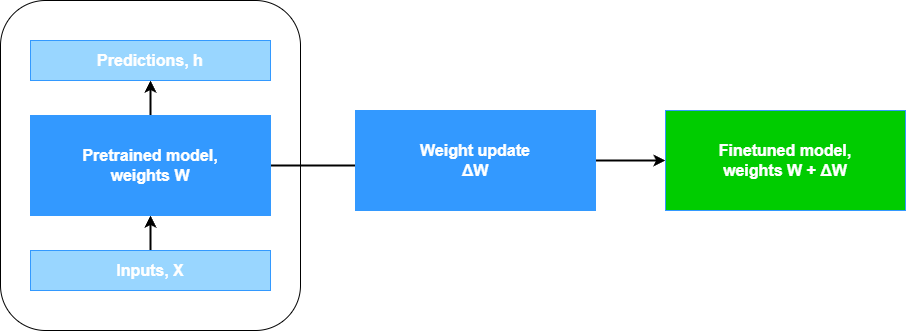
Eventually, compared to the original weights \(\mathbf{W}\), you end up with new weights \(\mathbf{W'}\) by adding \(\Delta \mathbf{W}\) to them. Like this:

\(\mathbf{W'} = \mathbf{W} + \Delta \mathbf{W}\)

Visually, that looks as follows:

Problems with finetuning large models

Let's now fast-forward a couple of years. BERT has been inspirational, but the world has moved on. Today, we're seeing a variety of very large foundation models, where...

A foundation model is a type of machine learning (ML) model that is pretrained to perform a range of tasks. Until recently, artificial intelligence (AI) systems were specialized tools, meaning that an ML model would be trained for a specific application or single use case (Red Hat, n.d.).

To put things into context:

• LLaMA, a foundation model for text, has 7 billion to 65 billion parameters.
• LLaMa, its successor, 2 has 7 to 70 billion parameters.
• Stable Diffusion, for generative images, has close to 1 billion parameters.

Still quite a large increase compared to these 110 to 340 million parameters for BERT!

Recall that you were fine-tuning your BERT model for a specific task. However, different news categories can provide different thresholds of newsworthiness. What's more, many newer foundation models exist today, so perhaps it's time to abandon BERT and see whether you can use a newer one.

Finetuning then becomes a bit problematic (Hu et al., 2021). Here's why that's the case:

1. Model training becomes really expensive: if you want to finetune the foundation model to your various news categories, then you'll have to train it multiple times, once for every category of news. This is really expensive.
2. Model storage becomes expensive, too: when you've finished training your model, you must store the weights. These are many gigabytes. You'll need a lot of storage if you want to store all these variants.

Introducing LoRA: Low-Rank Adaptation of large models

In a 2021 paper, Hu et al. introduce a new technique for finetuning models more cheaply. They call this method LoRA, for Low-Rank Adaptation of large models. It works by freezing the large model while adding a smaller set of weights which capture the weight update during fine-tuning, allowing you to finetune large models at a fraction of the computational cost. Let's dive into LoRA to see how it works by looking at:

• How weight updates during finetuning work.
• Matrices and their rank.
• Why LoRA is necessary given the weight matrices of large language models.
• How matrix decomposition works and how LoRA benefits from it when finetuning.

Weight updates during finetuning

Recall the weights change that we performed when finetuning the model:

\(\mathbf{W'} = \mathbf{W} + \Delta \mathbf{W}\)

It can be visualized as follows:

Here, \(\Delta \mathbf{W}\) is a \(\mathbf{M} \times \mathbf{N}\) matrix, where M is the number of rows and N the number of columns.

Matrices and their rank

A matrix also has what's known as a rank. The columns and the rows have a rank, and for simplicity it can be said that the rank of the matrix is the lowest of the two. Now, what's a rank, you say? It's the number of rows (or columns) that is unique. Suppose that we have this matrix:

\(\begin{matrix} 1 & 2 & 3 \\ 2 & 4 & 6 \end{matrix}\)

It is not unique - the second row is just the first one times two. Hence, this matrix has rank 1.

\( \begin{matrix} 1 & 2 & 3 \\ 2 & 5 & 6 \\ 3 & 5 & 9 \\ \end{matrix} \)

Here, even though the rows have rank 3 - the first and the third column aren't unique: the third is just the first times 3. So, here, the matrix has rank 2.

Why we're taking this side step is because the concept of full rank is really important. Wikipedia (n.d.) writes the following:

A matrix is said to have full rank if its rank equals the largest possible for a matrix of the same dimensions, which is the lesser of the number of rows and columns Wikipedia (n.d.).

In other words, if a \(3 \times 3\) matrix has rank 3, it's a full rank matrix.

The need for LoRA

Typically, when a large language model is pretrained, the weight matrices of the individual layers are full rank.

Here's where one of the core insights from the LoRA paper comes into view:

We take inspiration from Li et al. (2018a); Aghajanyan et al. (2020) which show that the learned over-parametrized models in fact reside on a low intrinsic dimension. We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”, leading to our proposed Low-Rank Adaptation (LoRA) approach (Hu et al., 2021).

In simpler English, what's written here is that even though such big, full-rank matrices were necessary to capture the full textual understanding during pretraining, finetuning requires much fewer weights. Why, you say? Because finetuning means using your model for one task only.

In other words, the authors of the LoRA paper theorize that many of the columns and rows of the large model will be non-unique after finetuning is finished. To be more precise, the weight matrices of the large model will no longer be full rank but rank-deficient, as it's called.

There must be something that we can do about that.

Decomposing matrices

Indeed, we can! A matrix can be decomposed into a product of matrices. This is the process of matrix decomposition.

Here's another matrix:

\( A = \begin{matrix} 2 & 3 \\ 1 & 4 \\ \end{matrix} \)

If it's decomposed it can be written as follows:

\( A = \begin{matrix} 1 & 0 \\ \frac{1}{2} & 1 \\ \end{matrix} \times \begin{matrix} 2 & 3 \\ 0 & 2\frac{1}{2} \\ \end{matrix}
\)

Benefiting from decomposed matrices

Suppose that we have a large language model that has a weight matrix \(\mathbf{W}\) of size \(700.000 \times 30.000\). Please note that in real neural networks models consist of many smaller matrices that together give the number of parameters, but for simplicity let's assume it has just one. In this case, the total amount of parameters would be 21B. Quite a lot - and training has just become really difficult on commodity hardware.

Recall that after finetuning, this matrix is theorized to be rank-deficient - or in plain English, that it will have many non-unique rows and/or columns!

So, this operation will produce a result that is rather inefficient:

\(\mathbf{W'} = \mathbf{W} + \Delta \mathbf{W}\)

But we know that matrices can be decomposed. Thus, we can also write the weight matrix as follows:

\(\mathbf{W} = \mathbf{A} \times \mathbf{B}\)

Here, \(\mathbf{A}\) would be a matrix of size \(700.000 \times r\) whereas \(\mathbf{B}\) would be one of size \(r \times 30.000\).

Also, \(r\) is a parameter that can be configured by the person training the model - in other words, it's a hyperparameter. The higher it is, the better the model will be able to capture complexities in the dataset better, but generally speaking it can be rather low due to the low intrinsic rank of finetuning.

In fact, the authors suggest that \(r\) can often be as low as 1 or 2 (Hu et al., 2021).

Let's now recompute the number of parameters necessary for finetuning the model. If \(r\) is 1, then the number of parameters would be just \(700.000 \times 1 + 1 \times 30.000 = 730.000\).

Less than one million parameters.

There would thus be way many fewer parameters to train, and the model would fine-tune on a fraction of the weights of the original model. This is why LoRA can allow you to finetune large models on hardware that can be considered commodity hardware.

Freezing the large model; training LoRA adapters

Now that we know how LoRA works via matrix decomposition, how is it implemented in actual finetuning?

First, the large language model is loaded in a pipeline for training. This can for example be a HuggingFace pipeline. Subsequently, its weights are frozen. This means that when finetuning is started, the weights of the large model remain the same.

Then, under the hood, a variety of small weight matrices are added to the layers, typically two per layer (the diagram below still assumes that our model has one matrix \(\mathbf{\Delta W}\) which is decomposed into \(\mathbf{A}\) and \(\mathbf{B}\), but real models have many such extra matrices, typically two per layer).

These matrices also go by the name of LoRA adapters. They are initialized differently (Hu et al., 2021). The \(\mathbf{A}\) matrices are initialized with Gaussian noise; the \(\mathbf{B}\) matrices with zeros.

We use a random Gaussian initialization for A and zero for B, so ∆W = BA is zero at the beginning of training (Hu et al., 2021).

This is beneficial, because \(\mathbf{\Delta W}\) will then be zero at the start of training, and the model weights will just equal \(\mathbf{W}\) i.e. the large language model after pretraining.

The finetuning process will alter these weights and will hopefully converge to a loss that is adequate for your language modelling goal.

Voila, that's how LoRA allows you to finetune large language models at very limited cost!

Swapping LoRA adapters for minimizing cost

Today, open source models have billions of weights, and proprietary variants are expected to go way beyond that. Now, imagine that you have multiple goals for which you'd like to employ language models. If you wouldn't use a technique like LoRA, storing all these weights takes quite a lot of space.

Additionally, you'll need many deployments of individual models, requiring quite a lot of memory.

With LoRA, this is made simpler: if you have finetuned for two different goals using the same large model, you can just swap the LoRA adapters and the behavior of your pipeline changes. This requires you to store the weights of your large model just once and the weights of LoRA adapters separately (but these are often quite small). Also, you can deploy the large model just once, and use different adapters whenever you need them.

References

• Devlin, J., Chang, M. W., Lee, K., & Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805. https://arxiv.org/abs/1810.04805
• Red Hat. (n.d.). Foundation models. Retrieved November 17, 2023, from https://www.redhat.com/en/topics/cloud-computing/foundation-models
• Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., ... & Chen, W. (2021). Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685. https://arxiv.org/abs/2106.09685
• Wikipedia contributors. (n.d.). Rank (linear algebra). In Wikipedia. Retrieved November 19, 2023, from https://en.wikipedia.org/wiki/Rank_(linear_algebra).