How to use L1, L2 and Elastic Net regularization with PyTorch?

Training a neural network means that you will need to strike a balance between optimization and over-optimization. Over-optimized models work really well on your training set, but due to their complexity - by taking the oddities within a training dataset as part of the mapping that is to be performed - they can fail really hard when the model is used in production.

Regularization techniques can be used to mitigate these issues. In this article, we're going to take a look at L1, L2 and Elastic Net Regularization. Click on the previous link to understand them in more detail in terms of theory, because this article focuses on their implementation in PyTorch. After reading it, you will...

• Understand why you need regularization in your neural network.
• See how L1, L2 and Elastic Net (L1+L2) regularization work in theory.
• Be able to use L1, L2 and Elastic Net (L1+L2) regularization in PyTorch, by means of examples.

Ready? Let's take a look! 😎

Why you need regularization

Training a neural network involves creating a mapping between an array of input variables \(\textbf{x}\) to an independent variable, often called \(\text{y}\). Recall that a mapping between such variables can be expressed mathematically, and that a mapping is represented by a function - say, \(f\). In this case, the mapping of the actual function is as follows: \(\text{y}: f(\textbf{x})\).

The way the mapping is performed is dependent on the way that you create it, or fit it. For example, in the image below, we generated two such mappings using exactly the same input data - the set of points. The first is a polyfit with three degrees of freedom, creating the yellow line. The second has ten degrees of freedom, creating the blue line.

Which mapping is more realistic, you say? Yellow or blue?

If you said yellow, you're right. Such extremities in mappings that are visible in the blue one are often very unlikely to be true, and occur likely due to excessive sensitivity of the model to oddities in your data set.

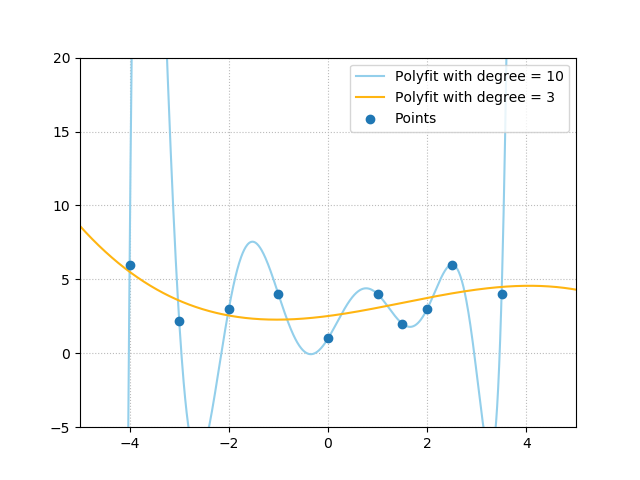
Training a neural network involves using your input data (the set of \(\textbf{x}\)s) to generate predictions for each sample (the corresponding set of \(\text{y}\). The network has trainable components that can jointly attempt to approximate the mapping, \(\text{y}: f(\textbf{x})\). The approximation is then called \(\hat{\text{y}}: f(\textbf{x})\), from y hat.

When feeding forward our samples and optimizing our model we do not know whether our model will learn a mapping like the one in yellow or the one in blue. Rather, it will learn a mapping that minimizes the loss value. This can lead to a situation where a mapping like the one in blue is learned, while such extremities are unwanted.

Adding regularization to your neural network, and specifically to the computed loss values, can help you in guiding the model towards learning a mapping that looks more like the one in yellow. After computing loss (i.e., the model error) after every forward pass, it adds another value to the loss function - and this value is higher when the model is more complex, while lower when it is less complex. In other words, the model is punished for complexity. This leads to a trained model that is as good as it can be when it is as simple as it can be at the same time.

Beyond Dropout, which is another mechanism for regularization, there are three main candidates that are used frequently:

• L1 Regularization, also called Lasso Regularization, involves adding the absolute value of all weights to the loss value.
• L2 Regularization, also called Ridge Regularization, involves adding the squared value of all weights to the loss value.
• Elastic Net Regularization, which combines L1 and L2 Regularization in a weighted way.

Now that we'll understand what regularization is and which key regularizers there are, you'll take a closer look at each - including examples for implementing them with PyTorch.

Let's get to work! 😎

Example of L1 Regularization with PyTorch

Suppose that you are using binary crossentropy loss with your PyTorch based classifier. You want to implement L1 Regularization, which effectively involves that \(\sum_f{ _{i=1}^{n}} | w_i |\) is added to the loss.

Here, \(n\) represents the number of individual weights, and you can see that we iterate over these weights. We then take the absolute value for each value \(w_i\) and sum everything together.

In other words, L1 Regularization loss can be implemented as follows:

\(\text{full_loss = original_loss + } \sum_f{ _{i=1}^{n}} | w_i |\)

Here, original_loss is binary crossentropy. However, it can be pretty much any loss function that you desire!

Implementing L1 Regularization with PyTorch can be done in the following way.

• We specify a class MLP that extends PyTorch's nn.Module class. In other words, it's a neural network using PyTorch.
• To the class, we add a def called compute_l1_loss. This is an implementation of taking the absolute value and summing all values for w in a particular trainable parameter.
• In the training loop specified subsequently, we specify a L1 weight, collect all parameters, compute L1 loss, and add it to the loss function before error backpropagation.
• We also print the L1 component of our loss when printing statistics.

Here is the full example for L1 Regularization with PyTorch:

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)

  def compute_l1_loss(self, w):
      return torch.abs(w).sum()


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare CIFAR-10 dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.CrossEntropyLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Compute L1 loss component
      l1_weight = 1.0
      l1_parameters = []
      for parameter in mlp.parameters():
          l1_parameters.append(parameter.view(-1))
      l1 = l1_weight * mlp.compute_l1_loss(torch.cat(l1_parameters))

      # Add L1 loss component
      loss += l1

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      minibatch_loss = loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.5f (of which %.5f L1 loss)' %
                (i + 1, minibatch_loss, l1))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Example of L2 Regularization with PyTorch

Implementing L2 Regularization with PyTorch is also easy. Understand that in this case, we don't take the absolute value for the weight values, but rather their squares. In other words, we add \(\sum_f{ _{i=1}^{n}} w_i^2\) to the loss component. In the example below, you can find how L2 Regularization can be used with PyTorch:

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)

  def compute_l2_loss(self, w):
      return torch.square(w).sum()


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare CIFAR-10 dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.CrossEntropyLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Compute l2 loss component
      l2_weight = 1.0
      l2_parameters = []
      for parameter in mlp.parameters():
          l2_parameters.append(parameter.view(-1))
      l2 = l2_weight * mlp.compute_l2_loss(torch.cat(l2_parameters))

      # Add l2 loss component
      loss += l2

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      minibatch_loss = loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.5f (of which %.5f l2 loss)' %
                (i + 1, minibatch_loss, l2))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Different way of adding L2 loss

L2 based weight decay can also be implemented by setting a delta value for weight_decay in the optimizer.

weight_decay (float, optional) – weight decay (L2 penalty) (default: 0)

PyTorch (n.d.)

For example:

optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4, weight_decay=1.0)

Example of Elastic Net (L1+L2) Regularization with PyTorch

It is also possible to perform Elastic Net Regularization with PyTorch. This type of regularization essentially computes a weighted combination of L1 and L2 loss, with the weights of both summing to 1.0. In other words, we add \(\lambda_{L1} \times \sum_f{ _{i=1}^{n}} | w_i | + \lambda_{L2} \times \sum_f{ _{i=1}^{n}} w_i^2\) to the loss component:

\(\text{full_loss = original_loss + } \lambda_{L1} \times \sum_f{ _{i=1}^{n}} | w_i | + \lambda_{L2} \times \sum_f{ _{i=1}^{n}} w_i^2 \)

In this example, Elastic Net (L1 + L2) Regularization is implemented with PyTorch:

• You can see that the MLP class representing the neural network provides two defs which are used to compute L1 and L2 loss, respectively.
• In the training loop, these are applied, in a weighted fashion (with weights of 0.3 and 0.7, respectively).
• The loss components are also printed on-screen when the statistics are printed.

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)

  def compute_l1_loss(self, w):
      return torch.abs(w).sum()

  def compute_l2_loss(self, w):
      return torch.square(w).sum()


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare CIFAR-10 dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.CrossEntropyLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Specify L1 and L2 weights
      l1_weight = 0.3
      l2_weight = 0.7

      # Compute L1 and L2 loss component
      parameters = []
      for parameter in mlp.parameters():
          parameters.append(parameter.view(-1))
      l1 = l1_weight * mlp.compute_l1_loss(torch.cat(parameters))
      l2 = l2_weight * mlp.compute_l2_loss(torch.cat(parameters))

      # Add L1 and L2 loss components
      loss += l1
      loss += l2

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      minibatch_loss = loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.5f (of which %.5f L1 loss; %0.5f L2 loss)' %
                (i + 1, minibatch_loss, l1, l2))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Summary

By reading this article, you have...

• Understood why you need regularization in your neural network.
• Seen how L1, L2 and Elastic Net (L1+L2) regularization work in theory.
• Been able to use L1, L2 and Elastic Net (L1+L2) regularization in PyTorch, by means of examples.

I hope that this article was useful for you! :) If it was, please feel free to let me know through the comments section 💬 Please let me know as well if you have any questions or other remarks. Where necessary, I will make sure to adapt the article.

What remains is to thank you for reading MachineCurve today. Happy engineering! 😎

Sources

PyTorch. (n.d.). Adam — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.optim.Adam.html#torch.optim.Adam

StackOverflow. (n.d.). L1 norm as regularizer in Pytorch. Stack Overflow. https://stackoverflow.com/questions/46797955/l1-norm-as-regularizer-in-pytorch