How to create a neural network for regression with PyTorch

In many examples of Deep Learning models, the model target is classification - or the assignment of a class to an input sample. However, there is another class of models too - that of regression - but we don't hear as much about regression compared to classification.

Time to change that. Today, we're going to build a neural network for regression. We will be using the PyTorch deep learning library for that purpose. After reading this article, you will...

• Understand what regression is and how it is different from classification.
• Be able to build a Multilayer Perceptron based model for regression using PyTorch.

Are you ready? Let's take a look!

What is regression?

Deep Learning models are systems of trainable components that can learn a mappable function. Such a function can be represented as \(\textbf{x} \rightarrow \text{y}\) at a high level, where some input \(\textbf{x}\) is mapped to an output \(\text{y}\).

Given the universal approximation theorem, they should even be capable of approximating any mathematical function! The exact mapping is learned through the high-level training process, in which example data that contains this mapping is fed through the model, after which the error is computed backwards and the model is optimized.

There is a wide variety of such mappings:

• An image of a cat represents to the class cat whereas a dog belongs to dog.
• The bounding box drawn here contains an object, whereas another one does not.
• And so forth.

These are all examples of classification. They answer whether a particular instance is present or not. Is that cat present? Yes or no. Is that dog present? Yes or no. Does it contain the object? Yes or no. You can compare such problems by assigning certain inputs to one or sometimes multiple bins.

Regression involves the same mappable function, but the output is not a bin-like (i.e. a discrete) value. Rather, the mappable function \(\textbf{x} \rightarrow \text{y}\) also converts the input data \(\textbf{x}\) to an output \(\text{y}\), but instead of a discrete value, \(\text{y}\) is continuous.

In other words, \(\text{y}\) can take any value that belongs to a particular range (for example, the real numbers). In other words, values such as \(\text{y} = 7.23\) or \(\text{y} = -12.77438\) are perfectly normal. Learning a model that maps an input \(\textbf{x}\) to a continuous target variable is a process called regression. It is now easy to see why such models are quite frequently used to solve numeric problems - such as predicting the yield of a crop or the expected risk level in a financial model.

Creating a MLP regression model with PyTorch

In a different article, we already looked at building a classification model with PyTorch. Here, instead, you will learn to build a model for regression. We will be using the PyTorch deep learning library, which is one of the most frequently used libraries at the time of writing. Creating a regression model is actually really easy when you break down the process into smaller parts:

1. Firstly, we will make sure that we import all the dependencies needed for today's code.
2. Secondly, we're going to ensure that we have our training data available. This data, which is the Boston Housing Dataset, provides a set of variables that may together ensure that a price prediction (the target variable) becomes possible.
3. Subsequently, the neural network will be created. This will be a Multilayer Perceptron based model, which is essentially a stack of layers containing neurons that can be trained.
4. The training dataset, which is by now represented as a torch.utils.data.Dataset, will need to be used in the model. The fourth step is to ensure that the dataset is prepared into a DataLoader, which ensures that data is shuffled and batched appropriately.
5. Then, we pick a loss function and initialize it. We also init the model and the optimizer (Adam).
6. Finally, we create the training loop, which effectively contains the high-level training process captured in code.

Let's get to work! 👩‍💻 Create a file or Notebook, e.g. regression-mlp.py, and write along :)

Today's dataset

The Boston House Prices Regression dataset contains 506 observations that relate certain characteristics with the price of houses (in $1000s) in Boston in some period.

Some observations about this data (from this article):

The minimum house price is $5000, while the maximum house price is $50.000. This may sound weird, but it’s not: house prices have risen over the decades, and the study that produced this data is from 1978 (Harrison & Rubinfeld, 1978). Actually, around 1978 prices of ≈$50.000 were quite the median value, so this dataset seems to contain relatively cheaper houses (or the Boston area was cheaper back then – I don’t know; Martin, 2017).

The mean house price was $22.533.

Variance in house prices is $84.587.

MachineCurve (2020)

These are variables available in the dataset:

CRIM per capita crime rate by town

ZN proportion of residential land zoned for lots over 25,000 sq.ft.

INDUS proportion of non-retail business acres per town

CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)

NOX nitric oxides concentration (parts per 10 million)

RM average number of rooms per dwelling

AGE proportion of owner-occupied units built prior to 1940

DIS weighted distances to five Boston employment centres

RAD index of accessibility to radial highways

TAX full-value property-tax rate per $10,000

PTRATIO pupil-teacher ratio by town

B 1000(Bk – 0.63)^2 where Bk is the proportion of blacks by town

LSTAT % lower status of the population

MEDV Median value of owner-occupied homes in $1000’s

MachineCurve (2020)

Obviously, MEDV is the median value and hence the target variable.

Imports

The first thing that we have to do is specifying the imports that will be used for today's regression model. First of all, we need torch, which is the representation of PyTorch in Python. We will also need its nn library, which is the neural networks library and contains neural network related functionalities. The DataLoader with which we will batch and shuffle the dataset is imported as well, and that's it for the PyTorch imports.

Next to PyTorch, we will also import two parts (the load_boston and StandardScaler components) from Scikit-learn. We will need them for loading and preparing the data; they represent as the source and a preparation mechanism, respectively.

import torch
from torch import nn
from torch.utils.data import DataLoader
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

Representing the Dataset

Above, you saw that we use Scikit-learn for importing the Boston dataset. Because it is not directly compatible with PyTorch, we cannot simply feed the data to our PyTorch neural network. For doing so, it needs to be prepared. This is actually quite easy: we can create a PyTorch Dataset for this purpose.

A PyTorch dataset simply is a class that extends the Dataset class; in our case, we name it BostonDataset. It has three defs: __init__ or the constructor, where most of the work is done, __len__ returning dataset length, and __getitem__ for retrieving an individual item using an index.

In the constructor, we receive X and y representing inputs and targets and possibly a scale_data variable for standardization, being True by default. We then check whether the data already has Tensor format - it really needs to be non-Tensor format to be processed. Subsequently, depending on whether we want our data to be standardized (which is smart), we apply the StandardScaler and immediately transform the data after fitting the scaler to the data. Next, we represent the inputs (X) and targets (y) as instance variables of each BostonDataset object.

class BostonDataset(torch.utils.data.Dataset):
  '''
  Prepare the Boston dataset for regression
  '''

  def __init__(self, X, y, scale_data=True):
    if not torch.is_tensor(X) and not torch.is_tensor(y):
      # Apply scaling if necessary
      if scale_data:
          X = StandardScaler().fit_transform(X)
      self.X = torch.from_numpy(X)
      self.y = torch.from_numpy(y)

  def __len__(self):
      return len(self.X)

  def __getitem__(self, i):
      return self.X[i], self.y[i]

Creating the neural network

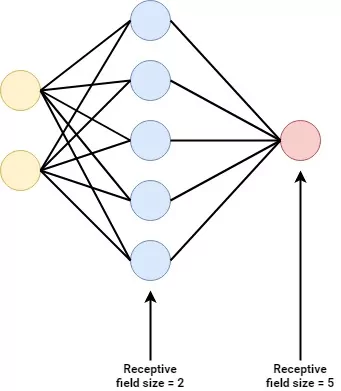
The regression model that we will create today will be a Multilayer Perceptron. It is the classic prototype of a neural network which you can see on the right as well.

In other words, a Multilayer Perceptron has multi_ple _layers of perceptrons. A Perceptron goes back into the 1950s and was created by an American psychologist named Frank Rosenblatt. It involves a learnable neuron which can learn a mapping between X and y.

Recall that this is precisely what we want to create. The Rosenblatt Perceptron, however, turned out to be incapable of mapping all possible functions - not surprising given the fact that it is one neuron only.

Multilayer Perceptrons change the internals of the original Perceptron and stack them in layers. In addition, they apply nonlinear activation functions to the individual neurons, meaning that they can also capture nonlinear patterns in datasets.

The result is that Multilayer Perceptrons can produce behavior that outperforms human judgment, although more recent approaches such as Convolutional Neural Networks and Recurrent Neural Networks are more applicable to some problems (such as computer vision and time series prediction).

Now, let's get back to writing some code. Our regression Multilayer Perceptron can be created by means of a class called MLP which is a sub class of the nn.Module class; the PyTorch representation of a neural network.

In the constructor (__init__), we first init the superclass as well and specify a nn.Sequential set of layers. Sequential here means that input first flows through the first layer, followed by the second, and so forth. We apply three linear layers with two ReLu activation functions in between. The first nn.Linear layer takes 13 inputs. This is the case because we have 13 different variables in the Boston dataset, all of which we will use (which may be suboptimal; you may wish to apply e.g. PCA first). It converts the 13 inputs into 64 outputs. The second takes 64 and generates 32, and the final one takes the 32 ReLU-activated outputs and learns a mapping between them and one output value.

Yep, that one output value is precisely the target variable that should be learned!

In the forward pass, we simply feed the input data (x) through the model (self.layers) and return the result.

class MLP(nn.Module):
  '''
    Multilayer Perceptron for regression.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Linear(13, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1)
    )


  def forward(self, x):
    '''
      Forward pass
    '''
    return self.layers(x)

Preparing the dataset

Now that we have specified a representation of the dataset and the model, it is time that we start using them.

if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Load Boston dataset
  X, y = load_boston(return_X_y=True)

The if statement written above means that the code following it will only run when the script is run with the Python interpreter. The first thing we do is fixing the initialization vector of our pseudorandom number generator, so that inconsistencies between random number generations will not yield to inconsistent end results.

Next, we actually use Scikit-learn's load_boston call to load the Boston housing dataset. The input data is assigned to the X variable while the corresponding targets are assigned to y.

We can next actually prepare our dataset in PyTorch format by creating a BostonDataset object with our training data. In other words, we will init the class that we created above!

Now that we have a PyTorch-compatible dataset, it still cannot be used directly. We will need to batch and shuffle the dataset first. This essentially means changing the order of the inputs and targets randomly, so that no hidden patterns in data collection can disturb model training. Following this, we generate batches of data - so that we can feed them through the model batched, given possible hardware constraints. We config the model to use 10 samples per batch, but this can be configured depending on your own hardware.

  # Prepare Boston dataset
  dataset = BostonDataset(X, y)
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

Picking a loss function

Recall from the high-level supervised training process that a loss function is used to compare model predictions and true targets - essentially computing how poor the model performs.

Picking a loss function thus has to be done relative to the characteristics of your data. For example, if your dataset has many outliers, Mean Squared Error loss may not be a good idea. In that case, L1 or Mean Average Error loss can be a better choice. In other words, first perform Exploratory Data Analysis on the variables you will be working with. Are there many outliers? Are the values close together? Depending on that, you will be able to pick an appropriate loss function to start with. Trial and error will tell whether you'll need to change after training a few times.

Initializing the model, loss function and optimizer

For the sake of simplicity, we will be using MAE loss (i.e., nn.L1Loss) today. Now that we have defined the MLP and prepared the data, we can initialize the MLP and the loss_function. We also initialize the optimizer, which adapts the weights of our model (i.e. makes it better) after the error (loss) was computed backwards. We will be using Adam, which is quite a standard optimizer, with a relatively default learning rate of 1e-4.

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.L1Loss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

Training loop

What remains is the creation of the training loop!

You can see that in this loop, the following happens:

• During training, we iterate over the entire training dataset for a fixed number of epochs. In today's model, we set the number of epochs to 5. This may be insufficient for minimization of loss in your model, but to illustrate how training works we set it to 5.
• At the start of every epoch, we set the value for current_loss (current loss in the epoch) to zero.
• Next, we iterate over the DataLoader. Recall that our data loader contains the shuffled and batched data. In other words, we iterate over all the batches - which have a maximum size of batch_size as configured above. The total number of batches is max(datasize_length / batch_size) (this means that if your batch_size is 10 and you'll have a dataset with 10006 samples, your number of batches will be 1001 - with the final batch having 6 samples only).
• We perform some conversions (e.g. Floating point conversion and reshaping) on the inputs and targets in the current batch.
• We then zero the gradients in the optimizer. This means that knowledge of previous improvements (especially important in batch > 0 for every epoch) is no longer available. This is followed by the forward pass, the error computation using our loss function, the backward pass, and finally the optimization.
• Found loss is added to the loss value for the current epoch. In addition, after every tenth batch, some statistics about the current state of affairs are printed.

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get and prepare inputs
      inputs, targets = data
      inputs, targets = inputs.float(), targets.float()
      targets = targets.reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

MLP for regression with PyTorch - full code example

It may be the case that you want to use all the code immediately.. In that case, here you go! :)

import torch
from torch import nn
from torch.utils.data import DataLoader
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

class BostonDataset(torch.utils.data.Dataset):
  '''
  Prepare the Boston dataset for regression
  '''

  def __init__(self, X, y, scale_data=True):
    if not torch.is_tensor(X) and not torch.is_tensor(y):
      # Apply scaling if necessary
      if scale_data:
          X = StandardScaler().fit_transform(X)
      self.X = torch.from_numpy(X)
      self.y = torch.from_numpy(y)

  def __len__(self):
      return len(self.X)

  def __getitem__(self, i):
      return self.X[i], self.y[i]


class MLP(nn.Module):
  '''
    Multilayer Perceptron for regression.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Linear(13, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1)
    )


  def forward(self, x):
    '''
      Forward pass
    '''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Load Boston dataset
  X, y = load_boston(return_X_y=True)

  # Prepare Boston dataset
  dataset = BostonDataset(X, y)
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.L1Loss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get and prepare inputs
      inputs, targets = data
      inputs, targets = inputs.float(), targets.float()
      targets = targets.reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Summary

In this article, you have learned to...

• Understand what regression is and how it is different from classification.
• Build a Multilayer Perceptron based model for regression using PyTorch.

I hope that this article was useful for your understanding and growth! If it was, please let me know through the comments section below 💬 Please also let me know if you have any questions or suggestions for improvement. I'll try to adapt my article :)

Thank you for reading MachineCurve today and happy engineering! 😎

Sources

PyTorch. (n.d.). L1Loss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.L1Loss.html#torch.nn.L1Loss

MachineCurve. (2020, November 2). Why you can't truly create Rosenblatt's Perceptron with Keras – MachineCurve. https://www.machinecurve.com/index.php/2019/07/24/why-you-cant-truly-create-rosenblatts-perceptron-with-keras/

MachineCurve. (2021, January 12). Rosenblatt's Perceptron with Python – MachineCurve. https://www.machinecurve.com/index.php/2019/07/23/linking-maths-and-intuition-rosenblatts-perceptron-in-python/

MachineCurve. (2020, November 16). Exploring the Keras datasets – MachineCurve. https://www.machinecurve.com/index.php/2019/12/31/exploring-the-keras-datasets/