← Back to homepage

How to use PyTorch loss functions

July 19, 2021 by Chris

Loss functions are an important component of a neural network. Interfacing between the forward and backward pass within a Deep Learning model, they effectively compute how poor a model performs (how big its loss) is. In this article, we're going to cover how to use a variety of PyTorch loss functions for classification and regression.

After reading this article, you will...

Are you ready? Let's take a look! 😎

What is a loss function?

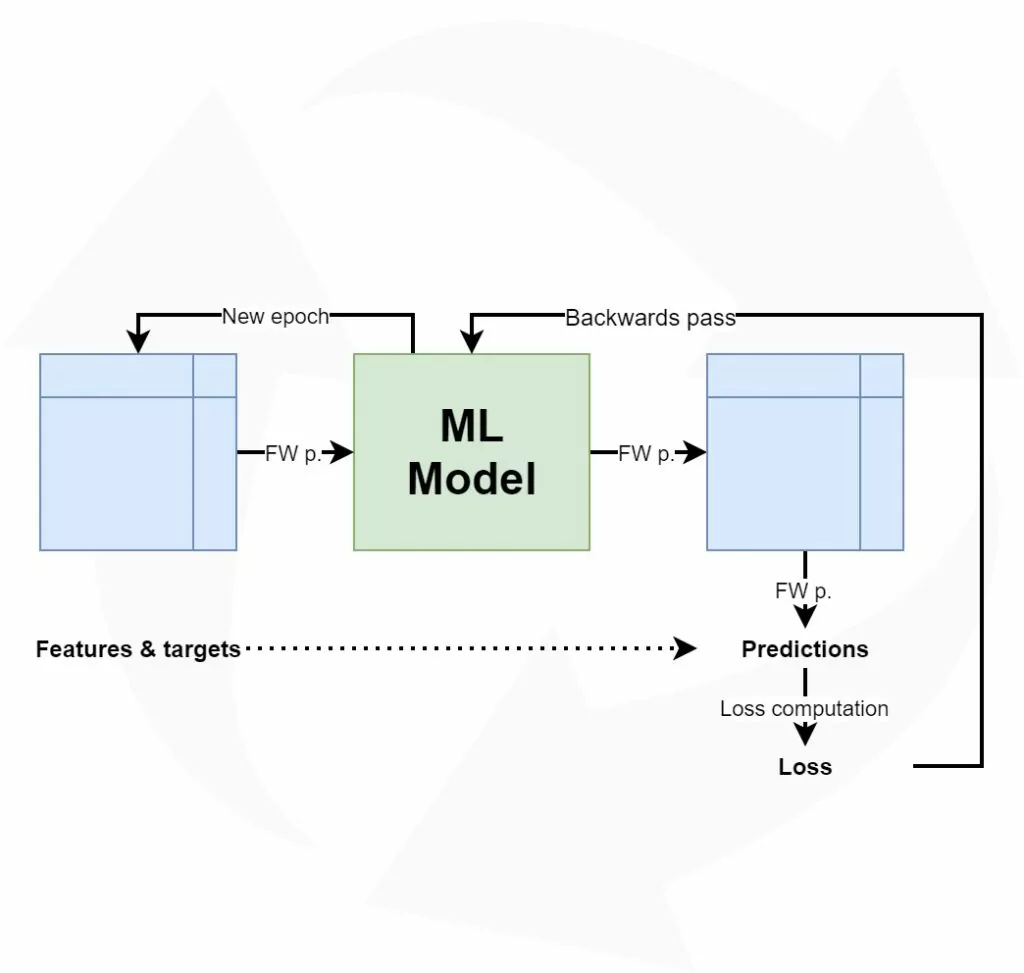
Training a Deep Learning model involves what I call a high-level training process. This process is visualized below. It all starts with a training dataset, which - in the case of classification and regression - contains a set of descriptive variables (features) that jointly are capable of predicting some target variable.

Training the Deep Learning model, which often is a neural network, involves sequentially performing a forward pass and a backward pass, followed by optimization. In the forward pass, the dataset is fed to the network (in a batched fashion). This leads to predictions for the targets, which can then be compared with the true labels. No prediction is perfect, and hence there will be an error value. Using this error value, the error can be computed backwards into the neural network using backpropagation. Subsequently, with an optimizer, the model can be changed slightly in the hope that it performs better next time. By repeating this process over and over again, the model can improve and learn to generate accurate predictions.

Let's get back to this error value. As the name suggests, it is used to illustrate how poorly the model performs. In Deep Learning jargon, this value is also called a loss value. It is computed by means of a loss function. There are many functions that can be used for this purpose. Choosing one depends on the problem you are solving (i.e. classification or regression), the characteristics of your dataset, and quite frequently on trial and error. In the rest of this article, we're going to walk through a lot of loss functions available in PyTorch. Let's take a look!

PyTorch Classification loss function examples

The first category of loss functions that we will take a look at is the one of classification models.

Binary Cross-entropy loss, on Sigmoid (nn.BCELoss) example

Binary cross-entropy loss or BCE Loss compares a target \(t\) with a prediction \(p\) in a logarithmic and hence exponential fashion. In neural network implementations, the value for \(t\) is either 0 or 1, while \(p\) can take any value between 0 and 1. This is the formula for binary cross-entropy loss:

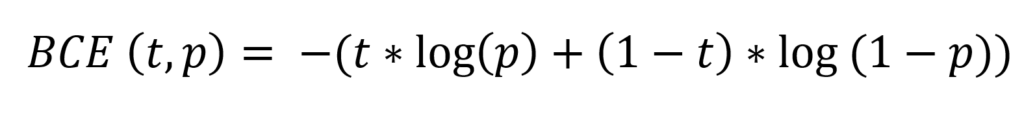
When visualizing BCE loss for a target value of 1, you can see that loss increases exponentially when the prediction approaches the opposite - 0, in our case.

This suggests that small deviations are punished albeit lightly, whereas big prediction errors are punished significantly.

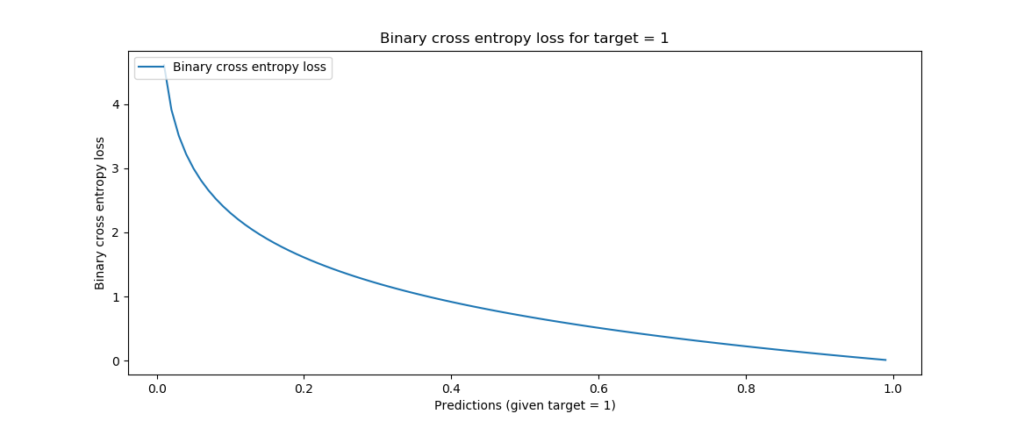
This makes binary cross-entropy loss a good candidate for binary classification problems, where a classifier has two classes.

Implementing binary cross-entropy loss with PyTorch is easy. It involves the following steps:

  1. Ensuring that the output of your neural network is a value between 0 and 1. Recall that the Sigmoid activation function can be used for this purpose. This is why we apply nn.Sigmoid() in our neural network below.
  2. Ensuring that you use nn.BCELoss() as your loss function of choice during the training loop.

A full example of using binary cross-entropy loss is given next, using the torchvision.datasets.FakeData dataset:

import os
import torch
from torch import nn
from torchvision.datasets import FakeData
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 3, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1),
      nn.Sigmoid()
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare FakeData dataset
  dataset = FakeData(size=15000, image_size=(3, 28, 28), num_classes=2, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=64, shuffle=True, num_workers = 4, pin_memory = True)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.BCELoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Prepare targets
      targets = targets \
                  .type(torch.FloatTensor) \
                  .reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Binary Cross-entropy loss, on logits (nn.BCEWithLogitsLoss)

Simple binary cross-entropy loss (represented by nn.BCELoss in PyTorch) computes BCE loss on the predictions \(p\) generated in the range [0, 1].

However, it is possible to generate more numerically stable variant of binary cross-entropy loss by combining the Sigmoid and the BCE Loss into one loss function:

This version is more numerically stable than using a plain Sigmoid followed by a BCELoss as, by combining the operations into one layer, we take advantage of the log-sum-exp trick for numerical stability.

PyTorch (n.d.)

This trick is summarized here.

In PyTorch, this is combined into the **nn.BCEWithLogitsLoss** function. The difference between nn.BCEWithLogitsLoss and nn.BCELoss is that BCE with Logits loss adds the Sigmoid function into the loss function. With simple BCE Loss, you will have to add Sigmoid to the neural network, whereas with BCE With Logits Loss you will not.

Here is an example demonstrating nn.BCEWithLogitsLoss using the torchvision.datasets.FakeData dataset:

import os
import torch
from torch import nn
from torchvision.datasets import FakeData
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 3, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare FakeData dataset
  dataset = FakeData(size=15000, image_size=(3, 28, 28), num_classes=2, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=64, shuffle=True, num_workers = 4, pin_memory = True)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.BCEWithLogitsLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Prepare targets
      targets = targets \
                  .type(torch.FloatTensor) \
                  .reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Negative log likelihood loss (nn.NLLLoss)

The previous two loss functions involved binary classification. In other words, they can be used for a classifier that works with two possible targets only - a class 0 and a class 1.

However, many classification problems involve more than two classes. The MNIST dataset (torchvision.datasets.MNIST) is a good example of such a classification problem: in MNIST, there is one class per digit, and hence there are 10 classes.

Negative log likelihood loss (represented in PyTorch as nn.NLLLoss) can be used for this purpose. Sometimes also called categorical cross-entropy, it computes the negative log likelihood of each prediction, and multiplies each log prediction with the true target value.

For example, if we have a three-class classification problem with a sample where the third target class is the true target class, our target vector is as follows: [0 0 1].

Say that our model predicts a 60% likelihood that it's the second class: [0.3 0.6 0.1]. In that case, our negative log likelihood loss is as follows:

-(0 * log(0.3) + 0 * log(0.6) + 1 * log(0.1)) = 1

Now suppose that after a few more epochs, it successfully starts predicting the third: [0.3 0.2 0.5]. Ensure that loss now becomes 0.30. When it is even more confident (say [0.05 0.05 0.90]), loss is 0.045. In other words, using this loss, you can create a multiclass classifier

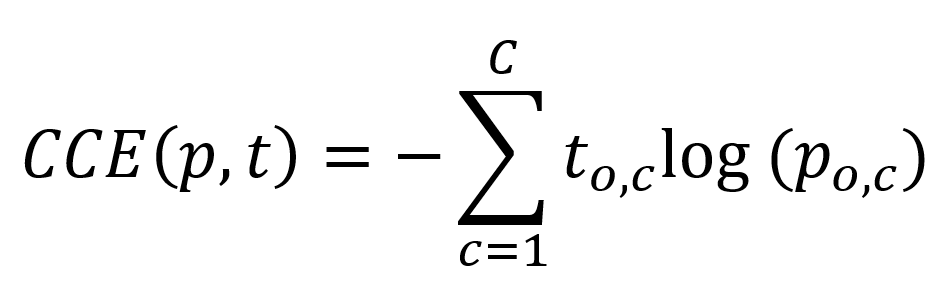
Note as well that by consequence, you can also model a binary classification problem this way: it is then a multiclass classification problem with two classes.

As you can see above, the prediction of our classifier should be a pseudo probability distribution over all the target classes. The softmax activation function serves this purpose. Using nn.NLLLoss therefore requires that we use a Softmax activated output in our neural network. nn.LogSoftmax is faster than pure nn.Softmax, however; that's why we are using nn.LogSoftmax in the nn.NLLLoss example for PyTorch below.

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10),
      nn.LogSoftmax(dim = 1)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare MNIST dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.NLLLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Cross-entropy loss (nn.CrossEntropyLoss)

Recall that nn.NLLLoss requires the application of a Softmax (or LogSoftmax) layer. As with the difference between BCELoss and BCEWithLogitsLoss, combining the Softmax and the NLLLoss into one likely allows you to benefit from computational benefits (PyTorch, n.d.). That's why you can also choose to use nn.CrossEntropyLoss instead.

This is an example of nn.CrossEntropyLoss with a PyTorch neural network. Note that the final layer does not use any Softmax related loss; this is already built into the loss function!

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare MNIST dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.CrossEntropyLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Poisson Negative log likelihood loss (nn.PoissonNLLLoss)

Suppose that your multiclass classification targets are drawn from a Poisson distribution (PyTorch, n.d.); that you already know this fact from your exploratory data analysis. You can then use the Poisson Negative log likelihood loss instead of regular nn.NLLLoss. In PyTorch (n.d.), this loss is described as follows:

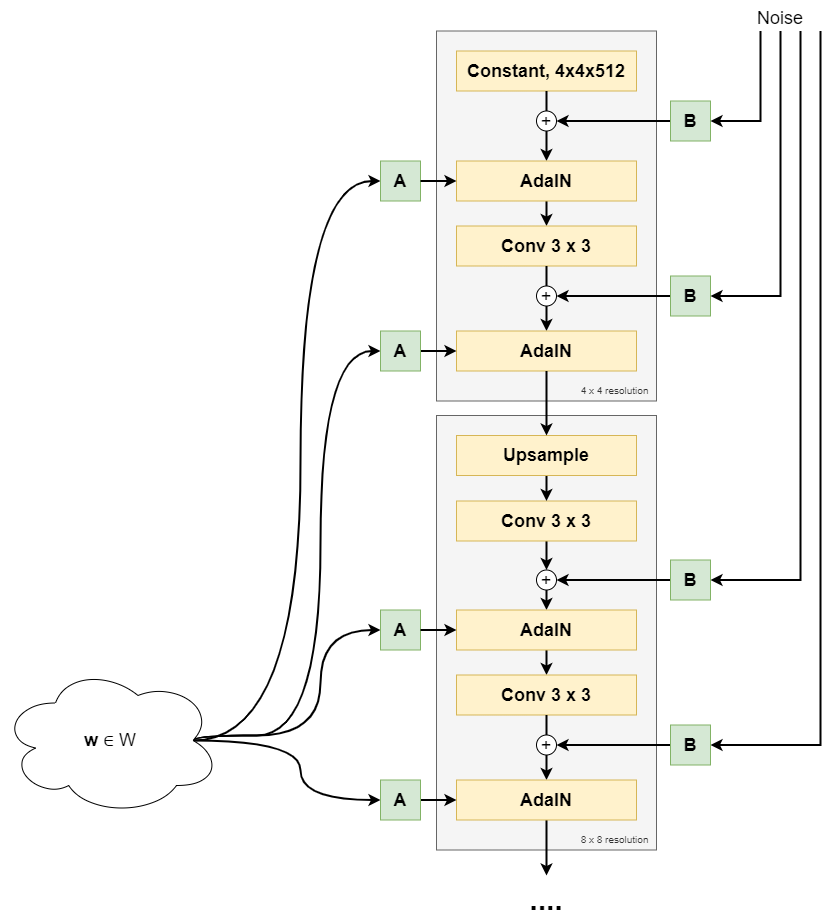
An example using Poisson Negative log likelihood loss with PyTorch is as follows:

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10),
      nn.LogSoftmax(dim = 1)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare MNIST dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.PoissonNLLLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Gaussian Negative log likelihood loss (nn.GaussianNLLLoss)

Suppose that your multiclass classification targets are drawn from a Gaussian distribution (PyTorch, n.d.). Loss can then be computed differently - by using the Gaussian Negative log likelihood loss. This loss function is represented within PyTorch (n.d.) as nn.GaussianNLLLoss.

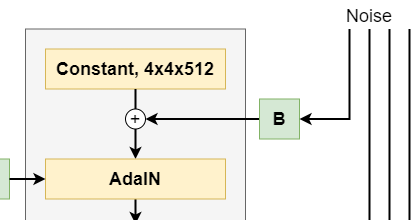
This is an example of using Gaussian Negative log likelihood loss with PyTorch.

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10),
      nn.LogSoftmax(dim = 1)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare MNIST dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.GaussianNLLLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Hinge embedding loss (nn.HingeEmbeddingLoss)

In PyTorch, the Hinge Embedding Loss is defined as follows:

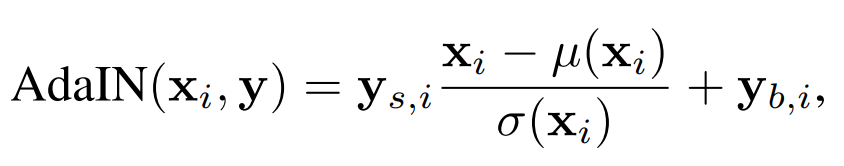
It can be used to measure whether two inputs (x and y) are similar, and works only if ys are either 1 or -1.

import os
import torch
from torch import nn
from torchvision.datasets import FakeData
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 3, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1),
      nn.Tanh()
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare FakeData dataset
  dataset = FakeData(size=15000, image_size=(3, 28, 28), num_classes=2, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=64, shuffle=True, num_workers = 4, pin_memory = True)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.HingeEmbeddingLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # For this example, change zero targets into -1
      targets[targets == 0] = -1

      # Prepare targets
      targets = targets \
                  .type(torch.FloatTensor) \
                  .reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Two-class soft margin loss (nn.SoftMarginLoss)

The two-class soft margin loss optimizes the following formula (PyTorch, n.d.):

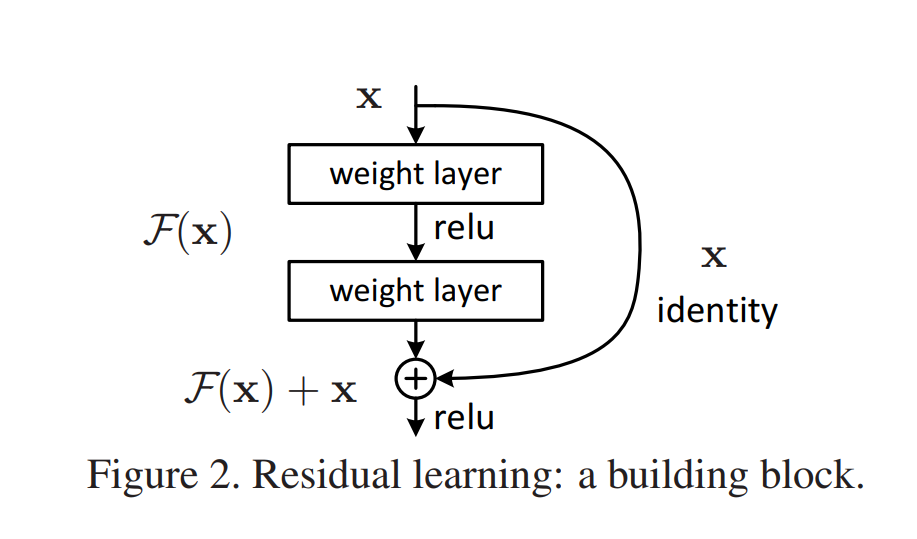
It can be used in binary classification problems as follows:

import os
import torch
from torch import nn
from torchvision.datasets import FakeData
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 3, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1),
      nn.Tanh()
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare FakeData dataset
  dataset = FakeData(size=15000, image_size=(3, 28, 28), num_classes=2, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=64, shuffle=True, num_workers = 4, pin_memory = True)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.SoftMarginLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # For this example, change zero targets into -1
      targets[targets == 0] = -1

      # Prepare targets
      targets = targets \
                  .type(torch.FloatTensor) \
                  .reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Multi-class margin loss (nn.MultiMarginLoss)

For multiclass classification problems, a multi-class hinge loss can be used represented by nn.MultiMarginLoss (PyTorch, n.d.):

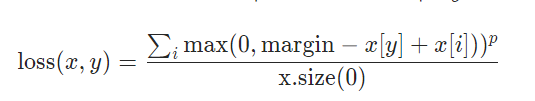
Here is an examplke using nn.MultiMarginLoss with PyTorch for multi-class single-label classification problems:

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10),
      nn.LogSoftmax(dim = 1)
    )


  def forward(self, x):
    '''Forward pass'''
    return self.layers(x)


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare MNIST dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.MultiMarginLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Multilabel soft margin loss (nn.MultiLabelSoftMarginLoss)

In multilabel classification problems, the neural network learns to predict multiple labels for an input sample. It can also be viewed as solving a tagging problem, as you are essentially assigning multiple tags (instead of just one class) to one input sample.

Multilabel soft margin loss (implemented in PyTorch as nn.MultiLabelSoftMarginLoss) can be used for this purpose. Here is an example with PyTorch. If you look closely, you will see that:

import os
import numpy as np
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 10)
    )


  def forward(self, x):
    '''
      Forward pass
      Note that 
    '''
    fp = self.layers(x)
    return fp


def draw_label(label):
  if label < 5:
    return [0, 0, 0, 1, 0, 0, 0, 1, 0, 0]
  if label < 8:
    return [1, 0, 0, 1, 0, 0, 0, 1, 0, 0]
  else:
    return [0, 0, 0, 0, 1, 0, 0, 1, 1, 0]

def replace_labels(labels):
  ''' Randomly replace labels '''
  new_labels = []
  for label in labels:
    new_labels.append(draw_label(label))
  return torch.from_numpy(np.array(new_labels))


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare MNIST dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.MultiLabelSoftMarginLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data
      targets = replace_labels(targets)

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Kullback-Leibler Divergence (KL Divergence) loss (nn.KLDivLoss)

KL Divergence can be used for Variational Autoencoders, multiclass classification and replacing Least Squares regression. Here is an example that uses KL Divergence with PyTorch:

import os
import numpy as np
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms

class MLP(nn.Module):
  '''
    Multilayer Perceptron.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Flatten(),
      nn.Linear(28 * 28 * 1, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1),
      nn.Sigmoid()
    )


  def forward(self, x):
    '''
      Forward pass
      Note that 
    '''
    fp = self.layers(x)
    return fp


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Prepare MNIST dataset
  dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.KLDivLoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get inputs
      inputs, targets = data
      targets = targets.float()

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 500 == 499:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

PyTorch Regression loss function examples

Let's now take a look at PyTorch loss functions for regression models.

Mean Absolute Error (MAE) / L1 Loss (nn.L1Loss)

Mean Absolute Error (MAE) is one of the loss functions for regression. This is what it looks like:

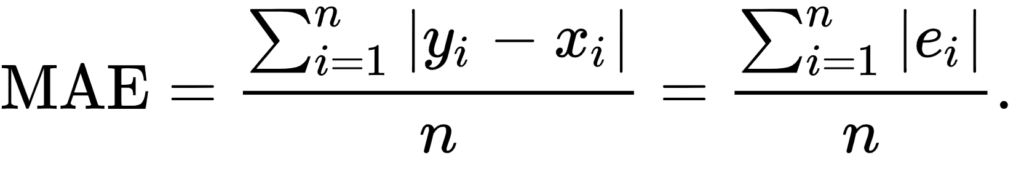
As you can see, it simply computes the difference between the input x and the expected value for y, then computing the absolute value (so that the outcome is always positive). It then averages this error.

Below, you will see an example of MAE loss (also called L1 Loss) within PyTorch, using nn.L1Loss and the Boston Housing dataset:

import os
import numpy as np
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

class BostonDataset(torch.utils.data.Dataset):
  '''
  Prepare the Boston dataset for regression
  '''

  def __init__(self, X, y, scale_data=True):
    if not torch.is_tensor(X) and not torch.is_tensor(y):
      # Apply scaling if necessary
      if scale_data:
          X = StandardScaler().fit_transform(X)
      self.X = torch.from_numpy(X)
      self.y = torch.from_numpy(y)

  def __len__(self):
      return len(self.X)

  def __getitem__(self, i):
      return self.X[i], self.y[i]


class MLP(nn.Module):
  '''
    Multilayer Perceptron for regression.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Linear(13, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1)
    )


  def forward(self, x):
    '''
      Forward pass
      Note that 
    '''
    fp = self.layers(x)
    return fp


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Load Boston dataset
  X, y = load_boston(return_X_y=True)

  # Prepare Boston dataset
  dataset = BostonDataset(X, y)
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.L1Loss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get and prepare inputs
      inputs, targets = data
      inputs, targets = inputs.float(), targets.float()
      targets = targets.reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Mean Squared Error (MSE) loss (nn.MSELoss)

The Mean Squared Error loss (or nn.MSELoss) essentially performs the same, but then doesn't compute the absolute value but rather the square of the difference. This also leads to the fact that all negatives are gone (squaring a negative value yields a positive one), but is better when the difference between errors is relatively small. Note that this comes at the cost of being sensitive to outliers.

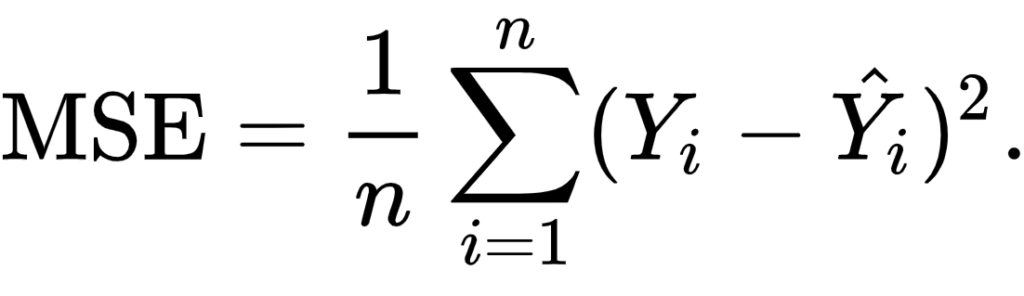
This is an example of using MSE Loss with PyTorch, which is provided as nn.MSELoss:

import os
import numpy as np
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

class BostonDataset(torch.utils.data.Dataset):
  '''
  Prepare the Boston dataset for regression
  '''

  def __init__(self, X, y, scale_data=True):
    if not torch.is_tensor(X) and not torch.is_tensor(y):
      # Apply scaling if necessary
      if scale_data:
          X = StandardScaler().fit_transform(X)
      self.X = torch.from_numpy(X)
      self.y = torch.from_numpy(y)

  def __len__(self):
      return len(self.X)

  def __getitem__(self, i):
      return self.X[i], self.y[i]


class MLP(nn.Module):
  '''
    Multilayer Perceptron for regression.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Linear(13, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1)
    )


  def forward(self, x):
    '''
      Forward pass
      Note that 
    '''
    fp = self.layers(x)
    return fp


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Load Boston dataset
  X, y = load_boston(return_X_y=True)

  # Prepare Boston dataset
  dataset = BostonDataset(X, y)
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.MSELoss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get and prepare inputs
      inputs, targets = data
      inputs, targets = inputs.float(), targets.float()
      targets = targets.reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Smooth MAE / L1 Loss (nn.SmoothL1Loss)

Recall from above that in comparison, MAE Loss (L1 Loss) works better when there are many outliers, while MSE Loss works better when there are few outliers and relatively small differences between errors. However, sometimes you want to use a loss function that is precisely in between these two. Smooth MAE Loss can then be used. Being provided as nn.SmoothL1Loss, the error is computed in a squared fashion if the error is smaller than a value for beta (i.e. benefiting from the MSE part). In all other cases, a value similar to the MAE is computed.

The beta parameter is configurable in the nn.SmoothL1Loss(...) initialization.

import os
import numpy as np
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

class BostonDataset(torch.utils.data.Dataset):
  '''
  Prepare the Boston dataset for regression
  '''

  def __init__(self, X, y, scale_data=True):
    if not torch.is_tensor(X) and not torch.is_tensor(y):
      # Apply scaling if necessary
      if scale_data:
          X = StandardScaler().fit_transform(X)
      self.X = torch.from_numpy(X)
      self.y = torch.from_numpy(y)

  def __len__(self):
      return len(self.X)

  def __getitem__(self, i):
      return self.X[i], self.y[i]


class MLP(nn.Module):
  '''
    Multilayer Perceptron for regression.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Linear(13, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1)
    )


  def forward(self, x):
    '''
      Forward pass
      Note that 
    '''
    fp = self.layers(x)
    return fp


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Load Boston dataset
  X, y = load_boston(return_X_y=True)

  # Prepare Boston dataset
  dataset = BostonDataset(X, y)
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.SmoothL1Loss()
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get and prepare inputs
      inputs, targets = data
      inputs, targets = inputs.float(), targets.float()
      targets = targets.reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Huber loss (nn.HuberLoss)

Huber loss is another loss function that can be used for regression. Depending on a value for delta, it is computed in a different way - put briefly, when errors are small, the error itself is part of the square, whereas it's the delta in the case of large errors:

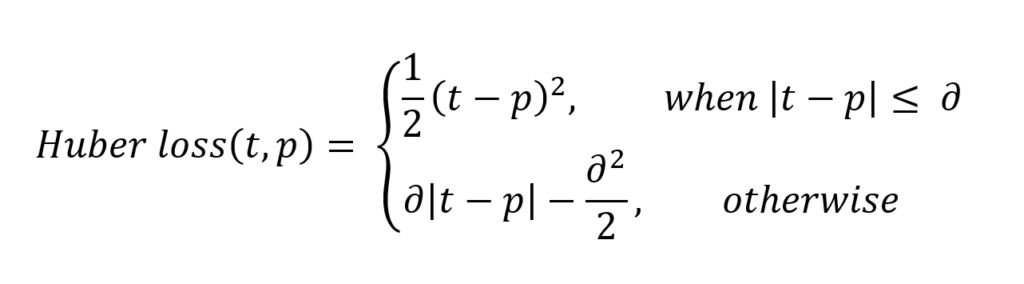
Visually, Huber loss looks as follows given different deltas:

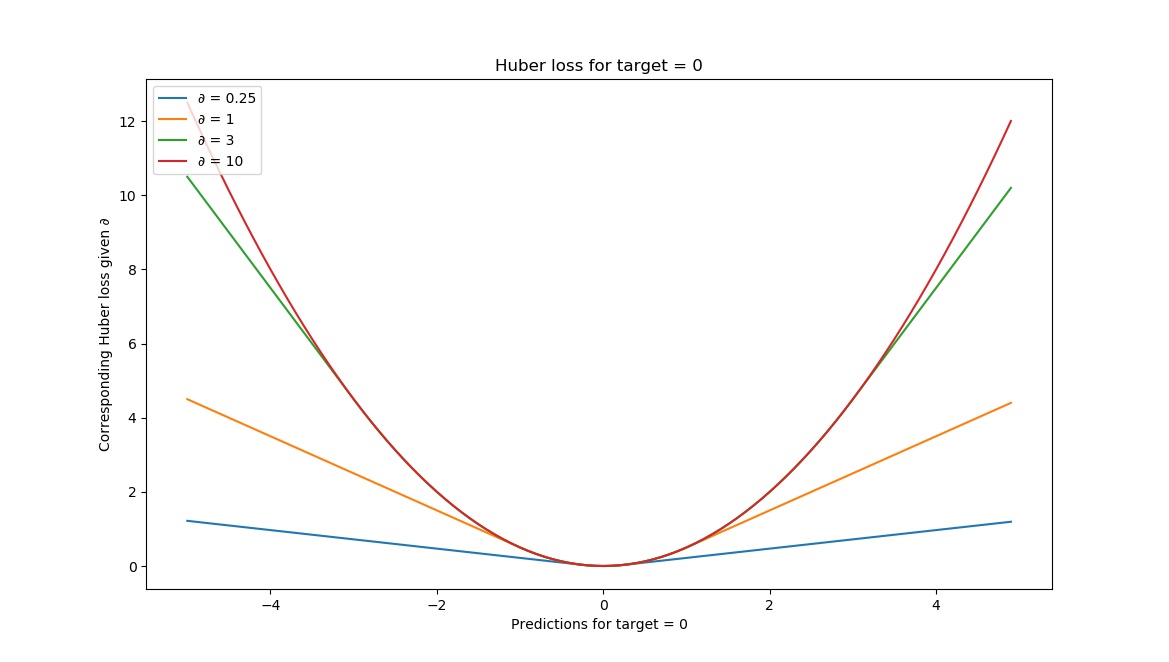
In other words, by tweaking the value for delta, we can adapt the loss function's sensitivity to outliers. It is therefore also a value that lies somewhere between MSE and MAE loss.

Being available as nn.HuberLoss (with a configurable delta parameter), it can be used in the following way:

import os
import numpy as np
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

class BostonDataset(torch.utils.data.Dataset):
  '''
  Prepare the Boston dataset for regression
  '''

  def __init__(self, X, y, scale_data=True):
    if not torch.is_tensor(X) and not torch.is_tensor(y):
      # Apply scaling if necessary
      if scale_data:
          X = StandardScaler().fit_transform(X)
      self.X = torch.from_numpy(X)
      self.y = torch.from_numpy(y)

  def __len__(self):
      return len(self.X)

  def __getitem__(self, i):
      return self.X[i], self.y[i]


class MLP(nn.Module):
  '''
    Multilayer Perceptron for regression.
  '''
  def __init__(self):
    super().__init__()
    self.layers = nn.Sequential(
      nn.Linear(13, 64),
      nn.ReLU(),
      nn.Linear(64, 32),
      nn.ReLU(),
      nn.Linear(32, 1)
    )


  def forward(self, x):
    '''
      Forward pass
      Note that 
    '''
    fp = self.layers(x)
    return fp


if __name__ == '__main__':

  # Set fixed random number seed
  torch.manual_seed(42)

  # Load Boston dataset
  X, y = load_boston(return_X_y=True)

  # Prepare Boston dataset
  dataset = BostonDataset(X, y)
  trainloader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)

  # Initialize the MLP
  mlp = MLP()

  # Define the loss function and optimizer
  loss_function = nn.HuberLoss(delta=1.0)
  optimizer = torch.optim.Adam(mlp.parameters(), lr=1e-4)

  # Run the training loop
  for epoch in range(0, 5): # 5 epochs at maximum

    # Print epoch
    print(f'Starting epoch {epoch+1}')

    # Set current loss value
    current_loss = 0.0

    # Iterate over the DataLoader for training data
    for i, data in enumerate(trainloader, 0):

      # Get and prepare inputs
      inputs, targets = data
      inputs, targets = inputs.float(), targets.float()
      targets = targets.reshape((targets.shape[0], 1))

      # Zero the gradients
      optimizer.zero_grad()

      # Perform forward pass
      outputs = mlp(inputs)

      # Compute loss
      loss = loss_function(outputs, targets)

      # Perform backward pass
      loss.backward()

      # Perform optimization
      optimizer.step()

      # Print statistics
      current_loss += loss.item()
      if i % 10 == 0:
          print('Loss after mini-batch %5d: %.3f' %
                (i + 1, current_loss / 500))
          current_loss = 0.0

  # Process is complete.
  print('Training process has finished.')

Summary

In this article, you have...

I hope that this article was useful to you! If it was, please feel free to drop a comment in the comments section 💬 Feel free to do the same if you have questions or other remarks.

Thank you for reading MachineCurve today and happy engineering! 😎

Sources

PyTorch. (n.d.). BCELoss — PyTorch 1.7.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.BCELoss.html

PyTorch. (n.d.). BCEWithLogitsLoss — PyTorch 1.8.1 documentation. https://pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html

PyTorch. (2019, March 7). Difference between cross-entropy loss or log likelihood loss? PyTorch Forums. https://discuss.pytorch.org/t/difference-between-cross-entropy-loss-or-log-likelihood-loss/38816/2

PyTorch. (n.d.). NLLLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html

PyTorch. (n.d.). CrossEntropyLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html

PyTorch. (n.d.). SoftMarginLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.SoftMarginLoss.html

PyTorch. (n.d.). HingeEmbeddingLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.HingeEmbeddingLoss.html#torch.nn.HingeEmbeddingLoss

PyTorch. (n.d.). MultiMarginLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.MultiMarginLoss.html

PyTorch. (n.d.). MultiLabelSoftMarginLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.MultiLabelSoftMarginLoss.html#torch.nn.MultiLabelSoftMarginLoss

PyTorch. (n.d.). MultiLabelMarginLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.MultiLabelMarginLoss.html#torch.nn.MultiLabelMarginLoss

MachineCurve. (2019, December 22). How to use kullback-leibler divergence (KL divergence) with Keras? https://www.machinecurve.com/index.php/2019/12/21/how-to-use-kullback-leibler-divergence-kl-divergence-with-keras/

PyTorch. (n.d.). HuberLoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.HuberLoss.html#torch.nn.HuberLoss

PyTorch. (n.d.). L1Loss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.L1Loss.html#torch.nn.L1Loss

PyTorch. (n.d.). MSELoss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.MSELoss.html#torch.nn.MSELoss

PyTorch. (n.d.). SmoothL1Loss — PyTorch 1.9.0 documentation. https://pytorch.org/docs/stable/generated/torch.nn.SmoothL1Loss.html#torch.nn.SmoothL1Loss

Hi, I'm Chris!

I know a thing or two about AI and machine learning. Welcome to MachineCurve.com, where machine learning is explained in gentle terms.

Getting started

Foundation models

Learn how large language models and other foundation models are working and how you can train open source ones yourself.

Keras

Keras is a high-level API for TensorFlow. It is one of the most popular deep learning frameworks.

TensorFlow

TensorFlow is the most popular deep learning framework. It is is used by many companies.

PyTorch

PyTorch is a deep learning framework which is popular for its ease of use and flexibility.

Machine learning theory

Read about the fundamentals of machine learning, deep learning and artificial intelligence.

Transformer architectures

Emerging since 2017, Transformer architectures are part of the state of the art in deep learning.

Most recent articles

January 8, 2024

LLM in a Flash: improving memory requirements of large language models

January 2, 2024

What is Retrieval-Augmented Generation?

December 27, 2023

Building a zero-shot image classifier with CLIP and HuggingFace Transformers

December 27, 2023

In-Context Learning: what it is and how it works

December 22, 2023

CLIP: how it works, how it's trained and how to use it

Article tags

bceloss
bcewithlogitsloss
binary crossentropy
categorical crossentropy
crossentropy
deep learning
hinge
hinge loss
huber loss
l1 loss
loss function
mae loss
margin loss
mse loss
neural networks
nllloss
pytorch
smooth l1 loss
softmarginloss

Most popular articles

February 18, 2020

How to use K-fold Cross Validation with TensorFlow 2 and Keras?

December 28, 2020

Introduction to Transformers in Machine Learning

December 27, 2021

StyleGAN, a step-by-step introduction

July 17, 2019

This Person Does Not Exist - how does it work?

October 26, 2020

Your First Machine Learning Project with TensorFlow 2.0 and Keras

Connect on social media

Connect with me on LinkedIn

To get in touch with me, please connect with me on LinkedIn. Make sure to write me a message saying hi!

See my work on GitHub

My work is available on GitHub. Feel free to check it out and see if it can be of use to you!

Side info

The content on this website is written for educational purposes. In writing the articles, I have attempted to be as correct and precise as possible. Should you find any errors, please let me know by creating an issue or pull request in this GitHub repository.

All text on this website written by me is copyrighted and may not be used without prior permission. Creating citations using content from this website is allowed if a reference is added, including an URL reference to the referenced article.

If you have any questions or remarks, feel free to get in touch.

TensorFlow, the TensorFlow logo and any related marks are trademarks of Google Inc.

PyTorch, the PyTorch logo and any related marks are trademarks of The Linux Foundation.

Montserrat and Source Sans are fonts licensed under the SIL Open Font License version 1.1.

Mathjax is licensed under the Apache License, Version 2.0.

Getting started

Foundation models

Learn how large language models and other foundation models are working and how you can train open source ones yourself.

Keras

Keras is a high-level API for TensorFlow. It is one of the most popular deep learning frameworks.

TensorFlow

TensorFlow is the most popular deep learning framework. It is is used by many companies.

PyTorch

PyTorch is a deep learning framework which is popular for its ease of use and flexibility.

Machine learning theory

Read about the fundamentals of machine learning, deep learning and artificial intelligence.

Transformer architectures

Emerging since 2017, Transformer architectures are part of the state of the art in deep learning.

Most popular articles

February 18, 2020

How to use K-fold Cross Validation with TensorFlow 2 and Keras?

December 28, 2020

Introduction to Transformers in Machine Learning

December 27, 2021

StyleGAN, a step-by-step introduction

July 17, 2019

This Person Does Not Exist - how does it work?

October 26, 2020

Your First Machine Learning Project with TensorFlow 2.0 and Keras

Side info

Connect with me on LinkedIn

To get in touch with me, please connect with me on LinkedIn. Make sure to write me a message saying hi!

See my work on GitHub

My work is available on GitHub. Feel free to check it out and see if it can be of use to you!

The content on this website is written for educational purposes. In writing the articles, I have attempted to be as correct and precise as possible. Should you find any errors, please let me know by creating an issue or pull request in this GitHub repository.

All text on this website written by me is copyrighted and may not be used without prior permission. Creating citations using content from this website is allowed if a reference is added, including an URL reference to the referenced article.

If you have any questions or remarks, feel free to get in touch.

TensorFlow, the TensorFlow logo and any related marks are trademarks of Google Inc.

PyTorch, the PyTorch logo and any related marks are trademarks of The Linux Foundation.

Montserrat and Source Sans are fonts licensed under the SIL Open Font License version 1.1.

Mathjax is licensed under the Apache License, Version 2.0.