One-Hot Encoding for Machine Learning with TensorFlow 2.0 and Keras

When you are training a Supervised Machine Learning model, you are effectively feeding forward data through the model, comparing the predictions, and improving the model internals - iteratively. These are mathematical operations and hence data must be numeric if we want to train a Neural network using TensorFlow and Keras. In many cases, this is the case. For example, images can be expressed as numbers; more specifically, the color values for the pixels of the image.

However, some datasets cannot be expressed as a number natively. For example, when you have features that represent group membership - for example, a feature called football club and where the contents can be FC Barcelona, Manchester United or AC Milan - the data is not numeric. Does this mean that we cannot use those for building a predictive model? No. On the contrary. We will show you how we can still use these features in TensorFlow and Keras models by using a technique called one-hot encoding. This article specifically focuses on that.

It is structured as follows. Firstly, we will take a look at one-hot encoding in more detail. What is it? How does it relate to categorical crossentropy loss, a type of loss that is used for training multiclass Neural Networks? Those are the questions that will provide the necessary context for applying one-hot encoding to a dataset. The latter is what we will show then, by giving you an example of applying one-hot encoding to a Keras dataset, covering how to use to_categorical when training a Neural Network step by step.

Let's take a look! 😎

What is One-Hot Encoding?

Before we dive into any practical part, I always tend to find it important that we know about what we are building. Hence, I think that it's important that we take a look at the concept of one-hot encoding in more detail first, and why it must be applied.

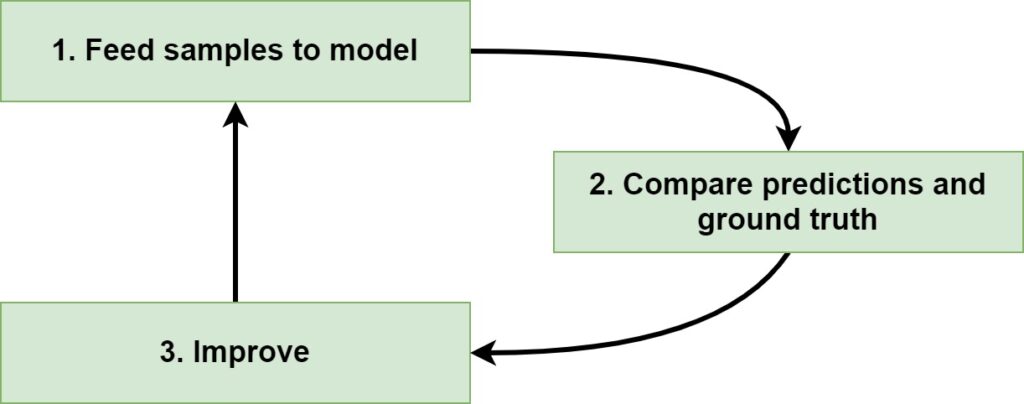
If you have read some other articles on MachineCurve (if not: click), you know that optimizing a Neural Network involves three main steps:

1. Feeding samples to the model, generating predictions. We call this the forward pass.
2. Comparing the predictions with the corresponding labels for the samples, also known as the ground truth. This results in a score illustrating how bad the model performs, also called the loss.
3. Improving the model by computing the individual contribution of model parameters to the loss and applying an optimizer to actually change the weights of the neural network.

We also know that step (1), feeding forward the samples through the model, involves a system of linear computations (\(\textbf{w} \times \textbf{x} + b\)) and mapping those to nonlinear outputs. Here, \(\textbf{w}\) represents the so-called weights vector, which captures (parts of) the patterns that have been learned by the Machine Learning model. \(\textbf{x}\) is also called the feature vector and represents a row from the input dataset. Bias is expressed as \(b\), and the activation function is often Rectified Linear Unit these days.

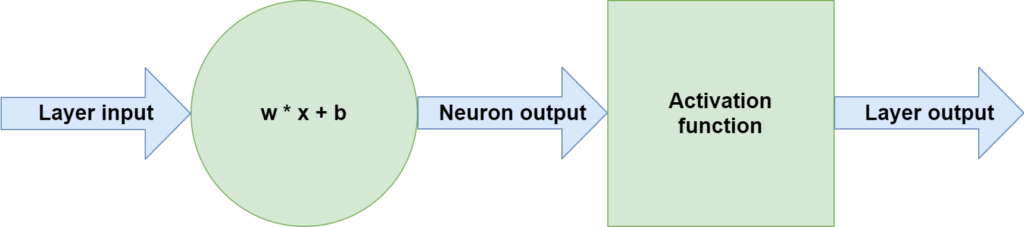
Clearly, from this overview, we can see that the linear operation involves a multiplication of two vectors and the addition of a scalar value. This all suggests that both \(\textbf{w}\), \(\textbf{x}\) and \(b\) must be numeric. And indeed: there is no such thing as a text-number vector multiplication that is used within Neural Networks, and hence indeed all data must be numeric.

There are many features that are numeric by nature:

• Age
• Time offset
• Pixel value for the pixel of an image

...and so on.

What to do when data isn't numeric

But not all data is numeric. For example, if we have a feature called Healthiness, we can either express one as being 'Healthy' or as 'Unhealthy'. This is text based data and hence conversion must take place if we want to use it in our Machine Learning model.

One-hot encoding is an approach that we can follow if we want to convert such non-numeric (but rather categorical) data into a usable format.

In digital circuits and machine learning, a one-hot is a group of bits among which the legal combinations of values are only those with a single high (1) bit and all the others low (0).

Wikipedia (2005)

In other words, we can express the categories into 'sets of bits' (recall that they can only take values between 0 and 1) so that for each set of bits, only one bit is true all the time, while all the others are zero. For example, for our Healthiness case, we can express the categories with two bits:

• \(\text{Healthy} \rightarrow [0 \ 1]\)
• \(\text{Unhealthy} \rightarrow [1 \ 0]\)

Really simple!

If we want to express more categories, we can simply add more bits. E.g. if we wanted to add the 'Unknown category', we would simply increase the number of bits that represent the one-hot encoding:

• \(\text{Healthy} \rightarrow [0 \ 0 \ 1]\)
• \(\text{Unhealthy} \rightarrow [0 \ 1 \ 0]\)
• \(\text{Unknown} \rightarrow [1 \ 0 \ 0]\)

Training Neural Networks with Categorical Crossentropy Loss

When we are training a Neural Network with TensorFlow, we always use categorical_crossentropy_loss when we are working with categorical data (and often, are trying to solve a multiclass classification problem).

As we can read on the page about loss functions, categorical crossentropy loss uses the prediction from our model for the true target to compute how bad the model performs. As we can read on that page as well, we see that this loss function requires data to be categorical - and hence, one-hot encoded.

How One-Hot Encoding fits CCE Loss

For this reason, it is desirable to work with categorical (and hence one-hot encoded) target data when we are using categorical crossentropy loss. This requires that we convert the targets into this format prior to training the Neural Network.

If we don't have one-hot encoded targets in the dataset, but integers instead to give just one example, it could be a good idea to use a different loss function. For example, sparse categorical crossentropy loss works with categorical targets where the targets are expressed as integer values, to give just an example. If you have a binary classification problem, and hence work with a Sigmoid activation function generating a prediction \( p \in [0, 1]\), you will want to use binary crossentropy loss instead.

One simple rule to remember: use categorical crossentropy loss when your Neural Network dataset has one-hot encoded target values!

Let's now take a look at how this works with a real example.

Using TensorFlow and Keras for One-Hot Encoding

TensorFlow is a widely used Machine Learning library for creating Neural Networks. Having been around for a while, it is one of the primary elements of the toolkit of a Machine Learning engineer (besides libraries like Scikit-learn and PyTorch). I'm quite fond of the library and have been using it for some time now. One of the main benefits is that it makes the life of Machine Learning engineers much easier.

TensorFlow is an end-to-end open source platform for machine learning. It has a comprehensive, flexible ecosystem of tools, libraries and community resources that lets researchers push the state-of-the-art in ML and developers easily build and deploy ML powered applications.

TensorFlow (n.d.)

The quote above states that "developers [can] easily build (...) ML powered applications". This is primarily due to the deep integration of the Keras library with TensorFlow, into tensorflow.keras. In the beginning of the TensorFlow era, TF provided its own APIs for constructing neural networks - and they are still available in tensorflow.nn. However, the learning curve for constructing them was steep and you had to have a lot of expertise when you wanted to create one. That's why Keras was born, an abstraction layer on top of TensorFlow (and originally also Theano and CNTK) with which people could easily build their Neural Networks.

The goal: speeding up iteration, as engineers should not have to worry about code, but rather about the principles - and hence the model structure - behind the code.

Today, TensorFlow and Keras are tightly coupled and deeply integrated, and the difference between the two is vastly disappearing. We will now use the Keras API within TensorFlow (i.e., tensorflow.keras) to construct a Convolutional Neural Network that is capable of classifying digits from the MNIST dataset. Let's go!

Taking a look at the MNIST dataset

The MNIST dataset? Although the odds are that you already know what this dataset is all about, there may be some readers who don't know about this dataset yet. As you can see below, it's a Computer Vision dataset - and it contains thousands of small grayscale images. More specifically, the images represent handwritten digits, and thus the numbers 0 to 9.

It is one of the most widely used datasets in Machine Learning education because it is so easy to use (as we shall see, it is embedded into Keras as tensorflow.keras.datasets.mnist) and because the classifiers that are trained on it perform really well. For this reason, we will be using MNIST as well today.

Loading data from the MNIST dataset is really easy. Let's open up a code editor, create a Python file and specify some imports - as well as a call to load_data(), with which we can load the MNIST dataset:

from tensorflow.keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)

If we run it, we see this text appear on screen after a while:

(60000, 28, 28)
(60000,)
(10000, 28, 28)
(10000,)

In other words, we can see that our training set contains 60000 28x28 samples (as the shape of one input value seems to be \((28, 28)\), we also see that our images are grayscale - if they were RGB, shape would have been \((28, 28, 3)\) per sample and hence \((60000, 28, 28, 3)\) for the whole array). Our testing set contains 10000 samples of the same format.

Inspecting a sample in more detail

Let's now inspect one sample in more detail.

index = 128
print(y_train[index])
print(y_train[index].shape)

The output is as follows:

1
()

We can see that the actual \(y\) value for index 128 is 1 - meaning that it represents the number 1. The shape is \(()\) and hence we are really talking about a scalar value.

If we would create a Neural Network, the best choice for this dataset would be to apply sparse categorical crossentropy loss - for the simple reason that we don't have to apply one-hot encoding if we use that loss function. Because we do want to show you how one-hot encoding works with TensorFlow and Keras, we do use categorical crossentropy loss instead, so we must apply one-hot encoding to the samples.

Applying One-Hot Encoding to the samples

If we need to convert our dataset into categorical format (and hence one-hot encoded format), we can do so using Scikit-learn's OneHotEncoder module. However, TensorFlow also offers its own implementation: tensorflow.keras.utils.to_categorical. It's a utility function which allows us to convert integer targets into categorical and hence one-hot encoded ones.

And if the library that you are using for building your Neural Network offers a one-hot encoder out of the box, why use Scikit-learn's variant instead? There is nothing wrong with the latter, but there would be simply no point in doing so :)

Now, let's add to the imports:

from tensorflow.keras.utils import to_categorical

And to the end of our code:

y_train = to_categorical(y_train)
y_test = to_categorical(y_test)

print(y_train[index])
print(y_train[index].shape)

The output for this part is now as follows:

[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
(10,)

We can clearly see that our target vector has ten values (by means of the \((10,)\) shape), one for each individual digit. The first is one while the others are zero, indicating that we are talking about the number 1, but then in one-hot encoded format. Exactly the same as our original integer value!

Creating a ConvNet that classifies the MNIST digits

Let's now clean up our code a bit. Make sure that it looks as follows:

• Import some modules that you need for the code.
• Load the MNIST dataset.
• Convert targets into one-hot encoded format.

# Imports
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical

# Load dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# Convert targets into one-hot encoded format
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)

We can now continue and add more code for constructing the actual ConvNet. Read here if you wish to receive more instructions about doing this; we'll simply show the code next.

# Imports
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical, normalize
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D
from tensorflow.keras.losses import categorical_crossentropy
from tensorflow.keras.optimizers import Adam
import numpy as np

# Load dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# Configuration options
no_classes = len(np.unique(y_train))
img_width, img_height = 28, 28
validation_split = 0.20
no_epochs = 25
verbosity = 1
batch_size = 250

# Reshape data
X_train = X_train.reshape(X_train.shape[0], img_width, img_height, 1)
X_test =  X_test.reshape(X_test.shape[0], img_width, img_height, 1)
input_shape = (img_width, img_height, 1)

# Convert targets into one-hot encoded format
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)

# Normalize the data
X_train = normalize(X_train)
X_test = normalize(X_test)

# Create the model
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=input_shape))
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dense(no_classes, activation='softmax'))

# Compile the model
model.compile(loss=categorical_crossentropy,
              optimizer=Adam(),
              metrics=['accuracy'])

# Fit data to model
model.fit(X_train, y_train,
          batch_size=batch_size,
          epochs=no_epochs,
          verbose=verbosity,
          validation_split=validation_split)

When running the code, we can see that our model starts training successfully:

Epoch 1/25
48000/48000 [==============================] - 12s 251us/sample - loss: 0.2089 - accuracy: 0.9361 - val_loss: 0.0858 - val_accuracy: 0.9738
Epoch 2/25
48000/48000 [==============================] - 36s 741us/sample - loss: 0.0555 - accuracy: 0.9828 - val_loss: 0.0607 - val_accuracy: 0.9821
Epoch 3/25
48000/48000 [==============================] - 45s 932us/sample - loss: 0.0295 - accuracy: 0.9905 - val_loss: 0.0605 - val_accuracy: 0.9807
Epoch 4/25
18500/48000 [==========>...................] - ETA: 25s - loss: 0.0150 - accuracy: 0.9957

Summary

Training Machine Learning models requires that your data is numeric. While this is true in many cases, some features represent groups of data - the categorical features. This is especially true for target values. In order to use them in your Machine Learning model, especially a Neural Network in the context of this article, you might want to one-hot encode your target data. This article looked at one-hot encoding in more detail.

Firstly, we looked at what one-hot encoding involves. More specifically, we saw that it allows us to convert categorical data expressed in integer format (e.g. the groups 'Healthy' and 'Unhealthy' in sets of bits where for each set just one value equals one and all the others equal zeros). This allows us to uniquely express groups and text based data for usage in Machine Learning models. We also looked at the necessity for categorical (and hence one-hot encoded) data when using categorical crossentropy loss, which is common in today's Neural Networks.

After finishing looking at theory, we moved forward to a practical example: showing how TensorFlow and Keras can be used for one-hot encoding a dataset. Specifically, using the TensorFlow to_categorical utility function, we saw how we can convert integer based targets for the MNIST dataset into one-hot encoded targets, after which categorical crossentropy loss is usable (as demonstrated by a neural network implemented towards the end). If you do however have such data, you might also wish to use sparse categorical crossentropy loss instead - there's no need to convert at all, but that was just done for the sake of this article.

I hope that you have learned something from today's article! If you did, please feel free to leave a comment in the comments section below 💬 Please do the same when you have any questions or other remarks. Regardless, thank you for reading MachineCurve today and happy engineering! 😎

References

Wikipedia. (2005, June 16). One-hot. Wikipedia, the free encyclopedia. Retrieved November 24, 2020, from https://en.wikipedia.org/wiki/One-hot

TensorFlow. (n.d.). https://www.tensorflow.org/