Which regularizer do I need for training my neural network?

There are three widely known regularization techniques for neural networks: L1 (or Lasso) regularization, L2 (or Ridge) regularization and Elastic Net regularization, which combines the two, and is also called L1+L2.

But which regularizer to use in your neural network? Especially for larger machine learning projects and for people who just started with machine learning, this is an often confusing element of designing your neural network.

In this blog post, I will try to make this process easier, by proposing a simple flowchart for choosing a regularizer for your neural network. It's based both on my experience with adding regularizers as well as what theory suggests about picking a regularization technique. If you have any suggestions, improvements or perhaps extensions, please feel free to share your experience by leaving a comment at the bottom of the page! 😊💬 Based on your feedback, we can improve the flowchart together.

The structure of this blog post is as follows. Firstly, we'll take a brief look at the basics of regularization - for starters, or for recap, if you wish. This includes a brief introduction to the L1, L2 and Elastic Net regularizers. Then, we continue with the flowchart - which includes the steps you could follow for picking a regularizer. Finally, we'll discuss each individual step in more detail, so that you can understand the particular order and why these questions are important.

Are you ready? Let's go! 😎

PS: If you wish to understand regularization or how to use regularizers with Keras in more detail, you may find these two blogs interesting as well:

• What are L1, L2 and Elastic Net Regularization in neural networks?
• How to use L1, L2 and Elastic Net Regularization with Keras?

The basics of regularization

Before we move on to my answer to the question which regularizer do I need, I think it's important to take one step back and look at the basics of regularization first. Through these basics, you'll likely understand the flowchart in a better way. If you already know a thing or two about regularizers, feel free to skip this part and directly move on to the flowchart.

Here, we'll cover these things:

• Why a regularizer could be necessary for your machine learning project;
• L1 Regularization;
• L2 Regularization;
• Elastic Net (L1+L2) Regularization.

Why a regularizer could be necessary

Firstly, let's take a look at why we need a regularizer in the first place. Suppose that we have a few data points from which we learn a regression model using a neural network:

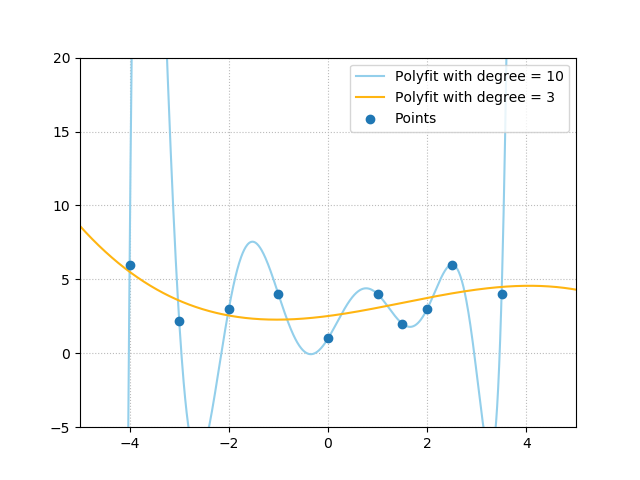
Which learnt mapping - i.e., the learnt function which maps the input data to the output data - would likely scale better to unseen data, the light blue one or the orange one? Obviouly, this depends on your data, but let's add a little bit of context: the data covers the weekly income versus the weekly net expense of a bank.

In that case, it's very unlikely that the light blue function is what we're looking for. The orange one looks quite nice though, and may even be representative of the actual real world pattern.

Unfortunately, training a machine learning model is a continuous balance between underfitting and overfitting, trying to find the sweet spot between a model that can be better in terms of predicting versus a model that predicts too well... for the training data, producing worse results for the data it hasn't seen yet. Especially when your model overfits, you'll see light blue-like curves starting to appear. You want to avoid this!

One way of doing so is by applying a regularizer to your model. A regularizer, by means of inclusion in the loss value that is minimized, punishes the model for being too complex. That is, it penalizes the states where the weights of your neural networks have too large and ideosyncratic values. This way, your weights remain simple, and you may find that the sensitivity of your model to overfitting is reduced.

Common regularizers

Now, which regularizers are out there? Let's take a look at the most common ones that are available for your machine learning projects today: L1, L2 and Elastic Net Regularization. Click here if you want to understand the regularizers in more detail.

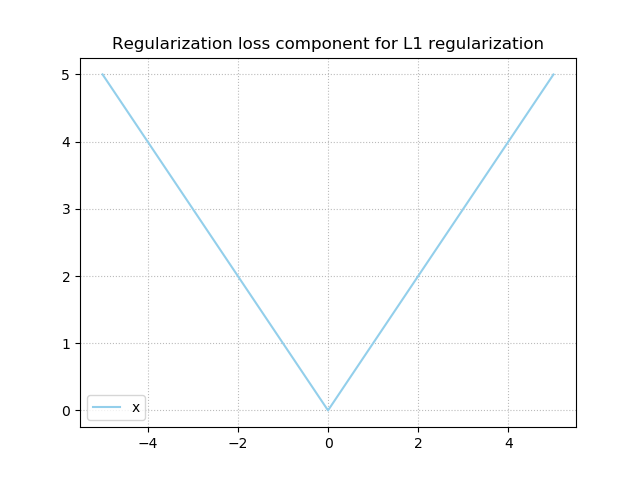
L1 Regularization

First of all, L1 Regularization, which is also called Lasso Regularization. By computing and summating the absolute values of weights, the so-called Taxicab norm (or L1 norm) is added to the loss value. This norm, which tells you something about the absolute distance across all dimensions that must be traveled from the origin to the tip of the weights vector, helps you to achieve simple models. What's more, because of the structure of the derivative (which produces constant values), weights that do not contribute sufficiently to the model essentially "drop out", as they are forced to become zero.

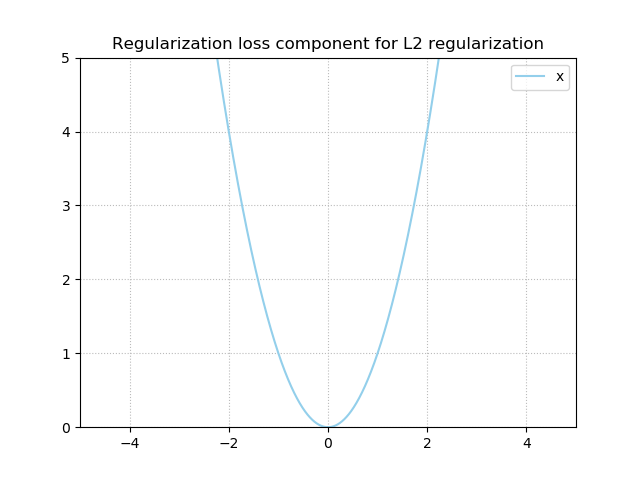
L2 Regularization

Secondly, there is L2 Regularization (a.k.a. Ridge Regularization), which is based on the summated squares of the weights. Although it does enforce simple models through small weight values, it doesn't produce sparse models, as the derivative - \(2x\) - produces smaller and smaller gradients (and hence changes) when \(x\) approaches zero. It can thus be useful to use L2 if you have correlative data, or when you think sparsity won't work for your ML problem at hand.

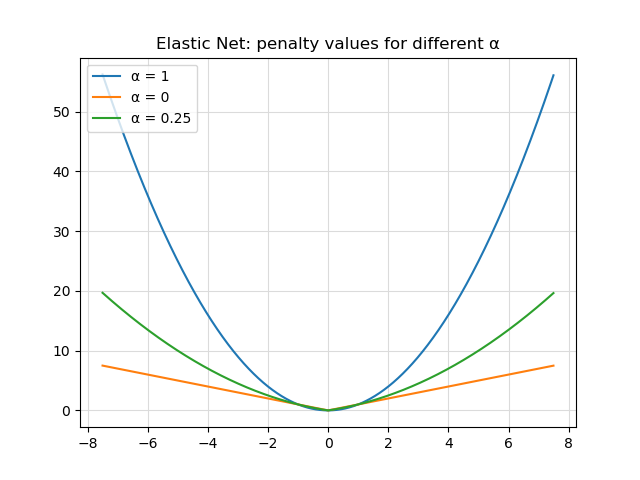
Elastic Net Regularization

When you combine L1 and L2 Regularization, you get Elastic Net Regularization. As you can see, depending on some hyperparameter (or two, if you don't combine the lambdas into the single alpha parameter) that can be configured by the machine learning engineer, it takes the shape of L1, or L2, or something in between. If you don't know which regularizer to apply, it may be worthwhile to try Elastic Net first, especially when you think that regularization may improve model performance over no regularization.

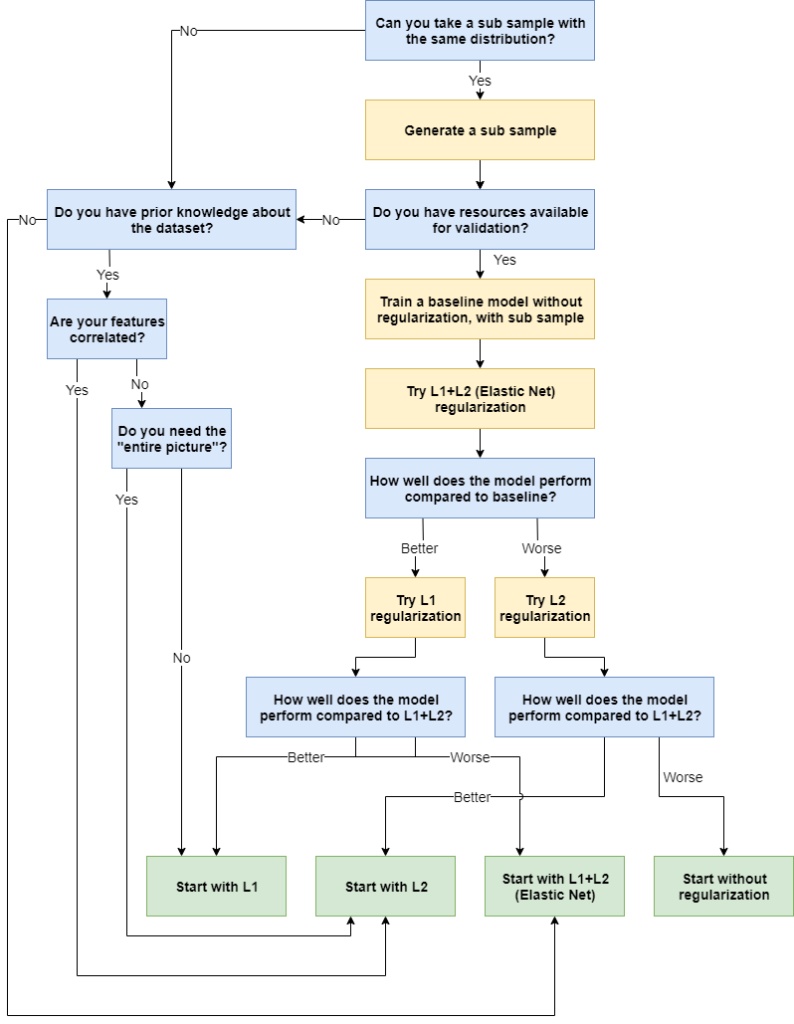
Picking a regularizer - a flowchart

Now that we have identified the three most common regularizers, here's a flowchart which can help you determine the regularizer that may be useful to your project. I always use these questions to help choose one:

• Can you take a subsample that has the same distribution as the main sample?
• Do you have resoures available for validation?
  • If so, how do the validation experiments perform?
• Do you have prior knowledge about your dataset?
  • Are your features correlated?
  • If not, do you need the "entire picture"?

In the next section, we'll analyze these questions individually, using more detail.

Now, here's the flowchart. Blue means that a question must be answered, yellow means that an action must be taken, and green means that you've arrived at an outcome.

Question to outcome - dissecting the flowchart

Let's now take a look at how we constructed the flow chart - and why I think that these questions help you choose a regularizer for your machine learning project.

Question 1: Can you take a sub sample with the same distribution?

Taking a sub sample of your dataset allows you to perform validation activities, i.e. to pick a likely adequate regularizer by testing up front. However, here, it's important to ensure that your sub sample has the same distribution (i.e. sample mean and sample variance) as the entire sample. This way, it will be most likely that good results achieved through validation generalize to the real training scenario.

Yes - take a sub sample and move to question 2

When you can take a sub sample with the same distribution, that would be preferred, as it opens the path to empirically determining which regularizer works best.

[Here is an algorithm that can be used for generating the sub sampl](https://maxhalford.github.io/blog/subsampling-a-training-set-to-match-a-test-set