When you're creating a neural network for classification, you're likely trying to solve either a binary or a multiclass classification problem. In the latter case, it's very likely that the activation function for your final layer is the so-called Softmax activation function, which results in a multiclass probability distribution over your target classes.

However, what is this activation function? How does it work? And why does the way it work make it useful for use in neural networks? Let's find out.

In this blog, we'll cover all these questions. We first look at how Softmax works, in a primarily intuitive way. Then, we'll illustrate why it's useful for neural networks/machine learning when you're trying to solve a multiclass classification problem. Finally, we'll show you how to use the Softmax activation function with deep learning frameworks, by means of an example created with Keras.

This allows you to understand what Softmax is, what it does and how it can be used.

Ready? Let's go! 😎

How does Softmax work?

Okay: Softmax. It always "returns a probability distribution over the target classes in a multiclass classification problem" - these are often my words when I have to explain intuitively how Softmax works.

But let's now dive in a little bit deeper.

What does "returning a probability distribution" mean? And why is this useful when we wish to perform multiclass classification?

Logits layer and logits

We'll have to take a look at the structure of a neural network in order to explain this. Suppose that we have a neural network, such as the - very high-level variant - one below:

The final layer of the neural network, without the activation function, is what we call the "logits layer" (Wikipedia, 2003). It simply provides the final outputs for the neural network. In the case of a four-class multiclass classification problem, that will be four neurons - and hence, four outputs, as we can see above.

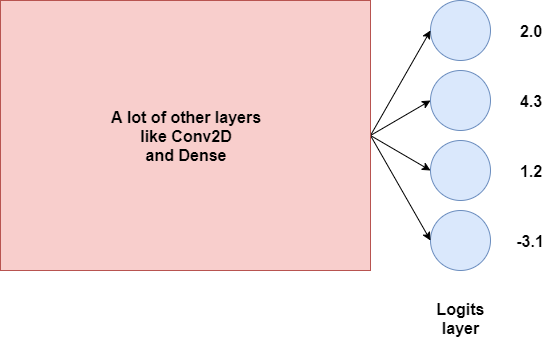
Suppose that these are the outputs, or our logits:

These essentially tell us something about our target classes, but from the outputs above, we can't make sense of it yet.... are they likelihoods? No, because can we have a negative one? Uh...

Multiclass classification = generating probabilities

In a way, however, predicting which target class some input belongs to is related to a probability distribution. For the setting above, if you would know the probabilities of the value being any of the four possible outcomes, you could simply take the \(argmax\) of these discrete probabilities and find the class outcome. Hence, if we could convert the logits above into a probability distribution, that would be awesome - we'd be there!

Let's explore this idea a little bit further :)

If we would actually want to convert our logits into a probability distribution, we'll need to first take a look at what a probability distribution is.

Kolmogorov's axioms

From probability theory class at university, I remember that probability theory as a whole can be described by its foundations, the so-called probability axioms or Kolmogorov's axioms. They are named after Andrey Kolmogorov, who introduced the axioms in 1933 (Wikipedia, 2001).

They are as follows (Wikipedia, 2001):

• The probability of something to happen, a.k.a. an event, is a non-negative real number.
• The probability that at least one of the events in the distribution occurs is 1, i.e. the sum of all the individual probabilities is 1.
• That the probability of a sequence of disjoint sets occurring equals the sum of the individual set probabilities.

For reasons of clarity: in percentual terms, 1 = 100%, and 0.25 would be 25%.

Now, the third axiom is not so much of interest for today's blog post, but the first two are.

From them, it follows that the odds of something to occur must be a positive real number, e.g. \(0.238\). Since the sum of probabilities must be equal to \(1\), no probability can be \(> 1\). Hence, any probability therefore lies somewhere in the range \([0, 1]\).

Okay, we can work with that. However, there's one more explanation left before we can explore possible approaches towards converting the logits into a multiclass probability distribution: the difference between a continuous and a discrete probability distribution.

Discrete vs continuous distributions

To deepen our understanding of the problem above, we'll have to take a look at the differences between discrete and continuous probability distribution.

According to Wikipedia (2001), this is a discrete probability distribution:

A discrete probability distribution is a probability distribution that can take on a countable number of values.

Wikipedia (2001): Discrete probability distribution

A continuous one, on the other hand:

A continuous probability distribution is a probability distribution with a cumulative distribution function that is absolutely continuous.

Wikipedia (2001): Continuous probability distribution

So, while a discrete distribution can take a certain amount of values - four, perhaps ;-) - and is therefore rather 'blocky' with one probability per value, a continuous distribution can take any value, and probabilities are expressed as being in a range.

Towards a discrete probability distribution

As you might have noticed, I already gave away the answer as to whether the neural network above benefits from converting the logits into a discrete or continuous distribution.

To play captain obvious: it's a discrete probability distribution.

For each outcome (each neuron represents the outcome for a target class), we'd love to know the individual probabilities, but of course they must be relative to the other target classes in the machine learning problem. Hence, probability distributions, and specifically discrete probability distributions, are the way to go! :)

But how do we convert the logits into a probability distribution? We use Softmax!

The Softmax function

The Softmax function allows us to express our inputs as a discrete probability distribution. Mathematically, this is defined as follows:

\(Softmax(x _i ) = \frac{exp(x_i)}{\sum{_j}^ {} {} exp(x_j))}\)

Intuitively, this can be defined as follows: for each value (i.e. input) in our input vector, the Softmax value is the exponent of the individual input divided by a sum of the exponents of all the inputs.

This ensures that multiple things happen:

• Negative inputs will be converted into nonnegative values, thanks to the exponential function.
• Each input will be in the interval \((0, 1)\).
• As the denominator in each Softmax computation is the same, the values become proportional to each other, which makes sure that together they sum to 1.

This, in return, allows us to "interpret them as probabilities" (Wikipedia, 2006). Larger input values correspond to larger probabilities, at exponential scale, once more due to the exponential function.

Let's now go back to the initial scenario that we outlined above.

We can now convert our logits into a discrete probability distribution:

| Logit value | Softmax computation | Softmax outcome | |