Weight initialization in neural networks: what is it?

An important predictor for deep learning success is how you initialize the weights of your model, or weight initialization in short. However, for beginning deep learning engineers, it's not always clear at first what it is - partially due to the overload of initializers available in contemporary frameworks.

In this blog, I will introduce weight initialization at a high level by looking at the structure of neural nets and the high-level training process first. Subsequently, we'll move on to weight initialization itself - and why it is necessary - as well as certain ways of initializing your network.

In short, you'll find out why weight initialization is necessary, what it is, how to do it - and how not to do it.

Update 18/Jan/2021: ensure that article is up to date in 2021. Also added a brief summary with the contents of the whole article at the top.

Summary: what is weight initialization in a neural network?

Neural networks are stacks of layers. These layers themselves are composed of neurons, mathematical units where the equation Wx + b is computed for each input. Here, x is the input itself, whereas b and W are representations for bias and the weights, respectively.

Both components can be used for making a neural network learn. The weights capture most of the available patterns hidden within a dataset, especially when they are considered as a system, i.e. as the neural network as a whole.

Using weights means that they must be initialized before the neural network can be used. We use a weight initialization strategy for this purpose. A poor strategy would be to initialize with zeros only: in this case, the input vector no longer plays a role, and the neural network cannot learn properly.

Another strategy - albeit a bit naïve - would be to initialize weights randomly. Very often, this works nicely, except in a few cases. Here, more advanced strategies like He and Xavier initialization must be used. We'll cover all of them in more detail in the rest of this article. Let's take a look!

The structure of a neural network

Suppose that we're working with a relatively simple neural net, a Multilayer Perceptron (MLP).

An MLP looks as follows:

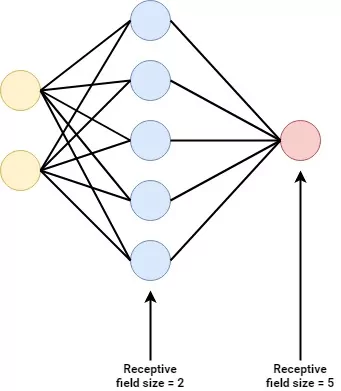
It has an input layer where data flows in. It also has an output layer where the prediction (be it classification or regression) flows out. Finally, there are one or multiple hidden layers which allow the network to handle complex data.

Mathematically, one of the neurons in the hidden layers looks as follows:

[mathjax]

\begin{equation} \begin{split} output &= \textbf{w}\cdot\textbf{x} + b \\ &=\sum_{i=1}^{n} w_nx_n + b \\ &= w_1x_1 + ... + w_nx_n + b \\ \end{split} \end{equation}

where \(\textbf{w}\) represents the weights vector, \(\textbf{x}\) the input vector and \(b\) the bias value (which is not a vector but a number, a scalar, instead).

When they are input, they are multiplied by means of a dot product. This essentially computes an element-wise vector multiplication of which subsequently the new vector elements are summated.

Your framework subsequently adds the bias value before the neuron output is complete.

It's exactly this weights vector that can (and in fact, must) be initialized prior to starting the neural network training process.

But explaining why this is necessary requires us to take a look at the high-level training process of a neural network first.

The high-level training process

Training a neural network is an iterative process. In the case of classification and a feedforward neural net such as an MLP, you'll make what is known as a forward pass and a backward pass. The both of them comprise one iteration.

In the forward pass, all training data is passed through the network once, generating one prediction per sample.

Since this is training data, we know the actual target and can compare them with our prediction, computing the difference.

Generally speaking, the average difference between prediction and target value over our entire training set is what we call the loss. There are multiple ways of computing loss, but this is the simplest possible way of imagining it.

Once we know the loss, we can start our backwards pass: given the loss, and especially the loss landscape (or, mathematically, the loss function), we can compute the error backwards from the output layer to the beginning of the network. We do so by means of backpropagation and use a process called gradient descent. If we know the error for an arbitrary neuron, we can adapt its weights slightly (controlled by the learning rate) to move a bit into the direction of the error. That way, over time, the neural network adapts to the data set it is being fed.

We'll cover these difficult terms in later blogs, since they do not further help explaining weight initialization, but together, they can ensure - given appropriate data - that neural networks show learning behavior over many iterations.

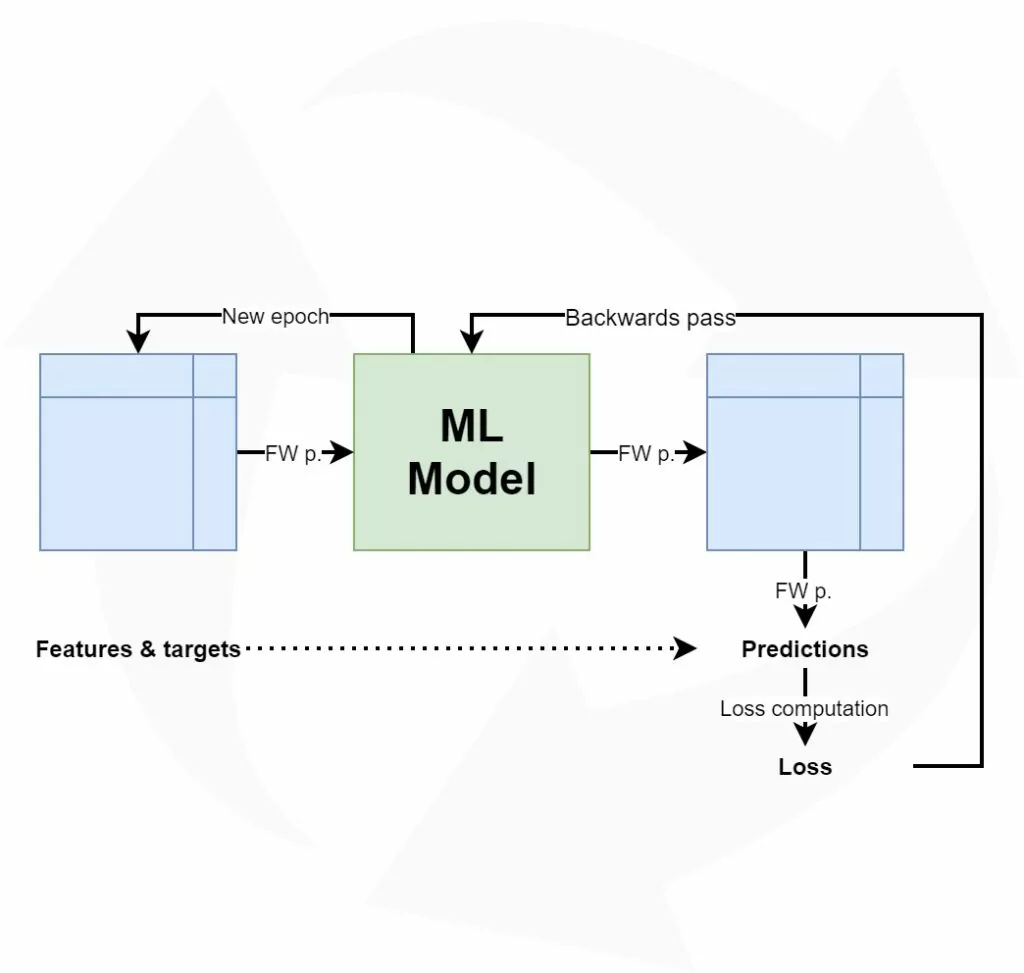
The high-level training process, showing a forward and a backwards pass.

Weight initialization

Now, we have created sufficient body to explain the need for weight initialization. Put very simply:

• If one neuron contains a weights vector that represents what a neuron has learnt that is multiplied with an input vector on new data;
• And if the learning process is cyclical, feeding forward all data through the network.

...it must start somewhere. And indeed, it starts at epoch 0 - or, put simply, at the start. And given the fact that during that first epoch, we'll see a forward pass, the network cannot have empty weights whatsoever. They will have to be initialized.

In short, weight initialization comprises setting up the weights vector for all neurons for the first time, just before the neural network training process starts. As you can see, indeed, it is highly important to neural network success: without weights, the forward pass cannot happen, and so cannot the training process.

Ways to initialize your network

Now that we have covered why weight initialization is necessary, we must look briefly into how to initialize your network. The reason why is simple: today's deep learning frameworks contain a quite wide array of initializers, which may or may not work as intended. Here, we'll slightly look into all-zeros initialization, random initialization and using slightly more advanced initializers.

All-zeros initialization

Of course, it is possible to initialize all neurons with all-zero weight vectors. However, this is a very bad idea, since effectively you'll start training your network while all your neurons are dead. It is considered to be poor practice by the deep learning community (Doshi, 2019).

Here's why:

Recall that in a neuron, \(output = \textbf{w}\cdot\textbf{x} + b\).

Or:

\begin{equation} \begin{split} output &= \textbf{w}\cdot\textbf{x} + b \\ &=\sum_{i=1}^{n} w_nx_n + b \\ &= w_1x_1 + ... + w_nx_n + b \\ \end{split} \end{equation}

Now, if you initialize \(\textbf{w}\) as an all-zeros vector, a.k.a. a list with zeroes, what do you think happens to \(w1 ... wn\)?

Exactly, they're all zero.

And since anything multiplied by zero is zero, you see that with zero initialization, the input vector \(\textbf{x}\) no longer plays a role in computing the output of the neuron.

Zero initialization would thus produce poor models that, generally speaking, do not perform better than linear ones (Doshi, 2019).

Random initialization

It's also possible to perform random initialization. You could use two statistical distributions for this: either the standard normal distribution or the uniform distribution.

Effectively, you'll simply initialize all the weights vectors randomly. Since they then have numbers > 0, your neurons aren't dead and will work from the start. You'll only have to expect that performance is (very) low the first couple of epochs, simply because those random values likely do not correspond to the actual distribution underlying the data.

With random initialization, you'll therefore see an exponentially decreasing loss, but then inverted - it goes fast first, and plateaus later.

There's however two types of problems that you can encouunter when you initialize your weights randomly: the vanishing gradients problem and the exploding gradients problem. If you initialize your weights randomly, two scenarios may occur:

• Your weights are very small. Backpropagation, which computes the error backwards, chains various numbers from the loss towards the updateable layer. Since 0.1 x 0.1 x 0.1 x 0.1 is very small, the actual gradient to be taken at that layer is really small (0.0001). Consequently, with random initialization, in the case of very small weights - you may encounter vanishing gradients. That is, the farther from the end the update takes place, the slower it goes. This might yield that your model does not reach its optimum in the time you'll allow it to train.
• In another case, you experience the exploding gradients scenario. In that case, your initialized weights are very much off, perhaps because they are really large, and by consequence a large weight swing must take place. Similarly, if this happens throughout many layers, the weight swing may be large: \(10^6 \cdot 10^6 \cdot 10^6 \cdot 10^6 = 10^\text{24}\). Two things may happen then: first, because of the large weight swing, you may simply not reach the optimum for that particular neuron (which often requires taking small steps). Second, weight swings can yield number overflows in e.g. Python, so that the language can no longer process those large numbers. The result, NaNs (Not a Number), will reduce the power of your network.

So although random initialization is much better than all-zeros initialization, you'll see that it can be improved even further.

Note that we'll cover the vanishing and exploding gradients problems in a different blog, where we'll also introduce more advanced initializers in large detail. For the scope of this blog, we'll stick at a higher level and will next cover two mitigators for those problems - the He and Xavier initializers.

Advanced initializers: He, Xavier

If you could reduce the vanishing gradients problem and the exploding gradients problem, how to do it?

That's exactly the question with which certain scholars set out in order to improve the initialization procedure for their neural networks.

Two initialization techniques are the result: Xavier (or Glorot) initialization, and He initialization.

Both work relatively similarly, but share their differences - that we will once again cover in another blog in more detail.

However, in plain English, what they essentially do is that they 'normalize' the initialization value to a value for which both problems are often no longer present. That means that very large initializations will be lowered significantly, while very small ones will be made larger. In effect, both initializers will attempt to produce values around one.

By consequence, modern deep learning practice often favors these advanced initializers - He initialization and Xavier (or Glorot) initialization - over pure random and definitely all-zeros initialization.

In this blog, we've seen why weight initialization is necessary, what it is and how to do it. If you have any questions, if you wish to inform me about new initializers or mistakes I made here... I would be really happy if you left a comment below 👇

Thank you and happy engineering! 😎

References

Chollet, F. (2017). Deep Learning with Python. New York, NY: Manning Publications.

Doshi, N. (2019, May 2). Deep Learning Best Practices (1) ? Weight Initialization. Retrieved from https://medium.com/usf-msds/deep-learning-best-practices-1-weight-initialization-14e5c0295b94

Neural networks and deep learning. (n.d.). Retrieved from http://neuralnetworksanddeeplearning.com/chap5.html

Wang, C. (2019, January 8). The Vanishing Gradient Problem. Retrieved from https://towardsdatascience.com/the-vanishing-gradient-problem-69bf08b15484